seungbeomdo

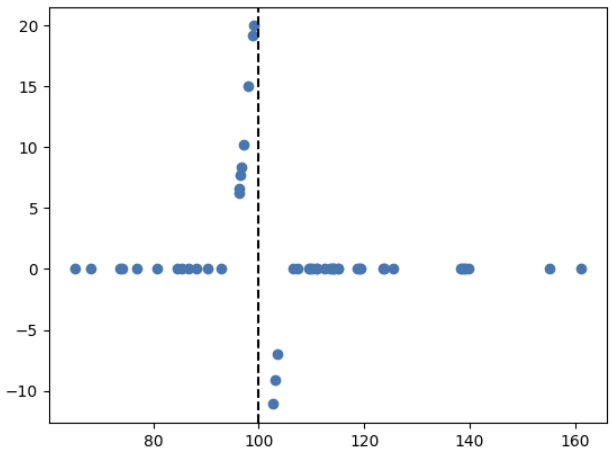
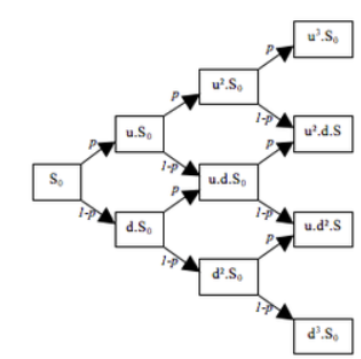
그럼 ELS도 델타헷지를 사용해서 만들 수 있을까? 이론적으로는 어렵다. 특히 배리어 터치 시 수익률 점프가 발생하는 부분을 복제하는 것이 이슈다. 이 부분은 특정 조건이 만족되었을 때 수익이 0 또는 H (0이 아닌 수)로 결정되는 Digital option이라고 할 수 있다. Digital call option은 기초자산 가격이 행사가격보다 클 때 고정된 cashflow를 지급하는 옵션이다. 예를 들어, 주가가 100 이상이면 50을 주고, 100 미만이면 0을 지급하는 디지털 콜옵션이 있다고 하자. 아래와 같은 payoff 구조를 갖는다. 이 부분을 델타 헷지로 구현해야 한다. 이는 이론적으로 불가능하다. 왜냐하면, Digital option의 델타는 $$\Delta_{digit} = H e^{-r..

모든 기업은 상품을 만들어서 판매한다. 증권사도 전통적인 의미의 제조업은 아니지만 어찌됐건 자기들이 취급하는 물건을 만들어서 판매한다. 증권사가 고객에게 금융상품을 판매하면, 일정한 조건이 만족되었을 때 고객에게 cashflow를 지급해야 한다. 그러므로 증권사가 만들어내는 것은 "일정한 조건이 만족되었을 때 발생하는 cashflow들의 뭉텅이"이다. 이 뭉텅이를 만들어내는 대표적인 기술이 델타 헷지(Delta Hedge)이다. 1. Delta Hedge의 이론적 배경 행사가격이 100인 유로피안 옵션을 팔았다고 하자(short). 그러면 증권사는 지금부터 주가가 100 이상일 때 "주가-100"을 지급할 준비를 해야 한다. 동시에 주가가 100 미만일 때는 "0"을 지급할 준비를 해야 한다. 가장 좋은..

홍콩 ELS 손실률 60% 육박…증권사 줄줄이 손실 공지 - SBS Biz 홍콩 ELS 손실률 60% 육박…증권사 줄줄이 손실 공지 [지난해 12월 서울 여의도 금융감독원 앞에서 열린 홍콩지수 ELS 피해자 집회. (사진=연합뉴스)]홍콩 H지수를 추종하는 주가연계증권(ELS) 상품의 대규모 원금 손실 우려가 현실화된 가운데 손실률 biz.sbs.co.kr 1. ELS의 정의 ELS가 화제다. ELS란 주가에 연계하여 수익을 지급하는 상품으로서, 국내 발행되는 파생상품들 중 가장 인기가 많다. 작년 한 해동안 발행된 규모가 40조원 정도가 된다. ELS의 정의는 현실에 비해 너무 일반적이다. 발행되는 ELS의 대부분은 (1) 일정한 수익을 지급하되, (2) 정해진 시점마다 조건에 의해 조기상환이 발생하며,..

이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021 www.pearson.com 이전 편 링크: Binomial Tree (1) 파생상품 가치평가 방법론 #4 Binomial Tree (1) Basic modeling 이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other ..

이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021 www.pearson.com 이전 편 링크: 주요 방법론 개요 파생상품 가치평가 방법론 #3 주요 방법론 개요 이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다..

이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021 www.pearson.com 이전 편 링크: 위험중립적 가치평가 파생상품 가치평가 방법론 #2 위험중립적 가치평가 (Risk-Neutral Valuation) 이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Deri..

이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021 www.pearson.com 이전 편: 파생상품의 "공정한 가격" 파생상품 가치평가 방법론 #1 파생상품의 "공정한 가격" 이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한..

이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 https://www.pearson.com/en-us/subject-catalog/p/options-futures-and-other-derivatives/P200000005938/9780136939917 Options, Futures, and Other Derivatives ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021 www.pearson.com 1. Motivation 가장 단순한 금융상품의 형태인 채권,..

DID 방법 (이중 차분 방법)- 처치집단과 통제집단 간의 차이 중 처치에 의한 효과(인과효과)를 식별하는 방법  카페에 들어가서 커피를 시켰는데, 사장님이 쿠폰을 받겠냐고 물어본다. 도장을 10개 찍으면 아메리카노 한 잔을 공짜로 받는 쿠폰이다.  고객 입장에서는 커피 1잔을 살 때마다 미래의 커피 1/10잔을 더 받게 되는 셈이므로 맛과 가격이 동일하다면 이 카페를 이용하는 것이 이득이 된다. 또한, 쿠폰을 기왕 받은 이상에 이 카페를 여러번 이용해야 이득을 실현할 수 있기 때문에 재방문 의향이 높아진다. 사장님은 이러한 고객의 의사결정 논리를 이해하고 재방문율(retention)을 높이기 위해 쿠폰 정책을 실시한다. 이 정책을 합리화하려면 다음의 AB 테스트가 필요하다.  커피쿠폰을 받지 않은 고객..

지난 편에서 보았듯이 동태적 패널 모형에 대해서는 임의효과 모형과 고정효과 모형이 항상 consistency를 만족하지 못한다. 따라서 동태적 패널 구조를 고려한 대안적인 추정방법이 필요하다. AH 추정: Anderson & Hsiao 동태적 회귀모형을 1계 차분하면 $$\Delta Y_{it} =\Delta \mathsf{X}_{it}\beta + \rho \Delta Y_{i,t-1}+\Delta\epsilon_{it}$$ 위 모형에서 $E(\Delta Y_{i,t-1} \Delta \epsilon_{i,t})≠0$이므로, 도구변수 방법(IV)을 고려해야 한다. 그럼 어떤 변수를 도구변수로 사용해야 할까? $\Delta Y_{i,t-1}$에 대한 도구변수는 $Y_{i,t-2}$를 사용하면 된다. 어떤..