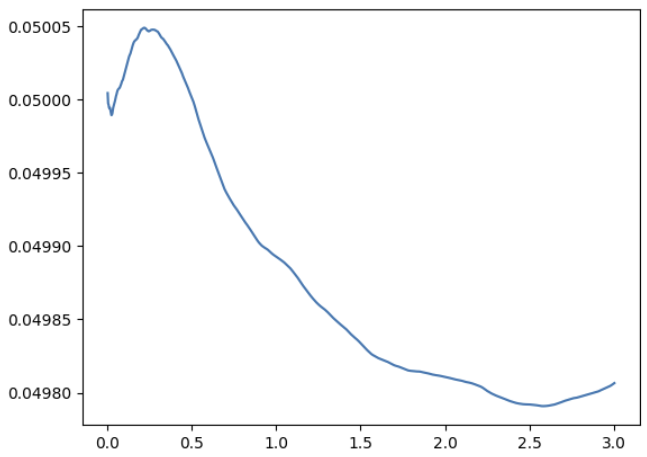
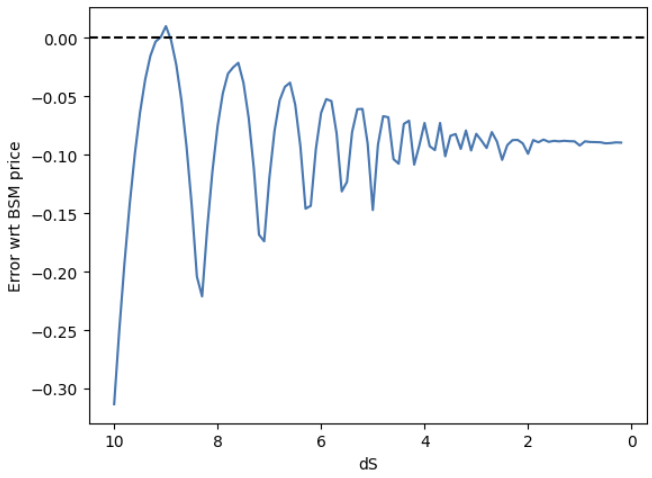
금리 파생상품이란 금리를 기초자산으로 하여 수익이 결정되는 파생상품을 말한다. 대부분 금융공학 교과서들을 보면 금리 파생상품을 설명할 때 다른 기초자산들보다 특별히 더 많은 분량을 할애하는 것을 알 수 있다. 그 이유는 크게 두 가지인데, 1) 금리의 확률과정은 더 복잡하다. 금리는 매크로 변수로서의 성격이 있기 때문에, 단지 기하적 브라운 운동만으로 나타내기 힘들다. 예를 들어 주가는 계속 상승할 수 있지만, 금리는 계속 상승하지 않고 일정 수준이 되면 다시 내려온다. 이를 mean-reverting이라고 한다. 2) 금리는 주가처럼 하나의 값이 아니라, 수익률 '곡선'으로서 존재한다. 기간 구조를 무시한 상태에서 그냥 "금리"라는 것은 존재하지 않는다. 따라서 금리를 추정할 때는 금리 커브 자체를 추..