seungbeomdo

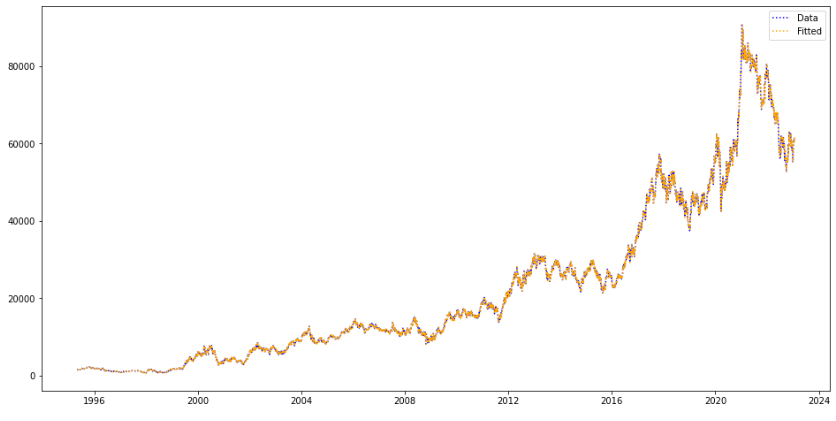
시계열 예측 모델링에 사용하는 Box-Jenkins-Method를 설명한다. 특별한 방법론이라기보다는, 전통적인 시계열 모델을 구현하는 데 있어서 사용하는 매뉴얼이라고 이해할 수 있다. 총 5가지 단계로 이루어지는데, 주어진 시계열의 정상성 여부를 테스트한다. 비정상 시계열일 경우 차분, 필터링 등 적당한 처리를 거쳐 정상화한다. ARMA 모델의 모수인 p와 q를 정한다. 모델의 계수들을 추정한다. 적합한 모델인지 알아보기 위해 계수 검정 및 잔차 검정을 실행한다. 최종 모델을 사용하여 예측한다. 이때 차분된 시계열을 역차분하여 원 시계열로 돌려준다. 그럼 한 단계씩 살펴보도록 하자. 1. 정상성 검정과 정상화 1.1. 정상성의 의의 첫 단계는 주어진 시계열의 정상성 여부를 파악하는 것이다. 간단한 방법..

이전 포스팅들에서 정상성의 정의, 시계열을 정상화하는 방법, 정상 시계열의 모델링 등등에 대해서 얘기해왔다. 여기서는 주어진 시계열의 정상성 여부를 어떻게 검정하는지 알아보자. 1. ADF 검정 정상성 검정의 한 가지 방법은 ADF 검정(Augmented Dickey-Fuller test)이다. 유사한 검정 방법으로 DF 검정이 있는데, ADF 검정이 DF 검정을 일반화한 것에 불과하므로 혼란스러울 필요는 없다. 1.1. ADF 검정의 아이디어: 단위근 ADF 검정의 아이디어를 살펴보자. 우선 모든 정상 시계열은 적당한 AR(p) process로 나타낼 수 있다고 가정한다. 즉 우리는 AR process의 틀 안에서 정상성을 검정하는 것임에 유의해야 한다. 그럼 MA process나 ARMA proces..

1. MA(1) 모형 1.1. MA(1) 모형의 정의 MA(Moving-Average) 모형은 현재 시점의 값을 과거 시점의 모형 오차로 회귀시키는 모형이다. 즉 시계열 $X_{t}$에 대하여, MA(1) 모형은 다음과 같다. $$X_{t} = c + \epsilon_{t} + {\theta}{\epsilon}_{t-1}$$ where c is a constant and $\epsilon_{t} \sim w.n.(0,\sigma^{2})$ 1.2. MA(1) 모형의 성질 MA(1) 모형을 따르는 시계열의 주요 모멘트들은 다음과 같다. $E[X_{t}] = c$ $Var[X_{t}] = (1+\theta^{2})\sigma^{2}$ $Cov(X_{t},X_{t-1}) = \theta\sigma^{2}$ $..

'정상' 시계열을 설명하기 위해 사용하는 대표적인 모형들을 정리한다. 1. 백색잡음(white noise) 백색잡음은 시계열 그 자체를 모델링하는 데 사용되지는 않는다. 하지만 모델링의 중요한 요소이고 살펴보아야할 성질이 있으므로 먼저 다룬다. 다음을 만족하는 $\epsilon_{t}$를 백색잡음이라고 한다. $E[\epsilon_{t}] = 0$, $Var[\epsilon_{t}] = \sigma^{2}$ and $Cov[\epsilon_{t}, \epsilon_{t-k}] = 0$ for k = 1, 2, 3, ... 보론) white noise와 IID를 구분해야 한다. white noise는 약정상성을 만족하고 자기공분산이 0이며, IID는 강정상성을 만족하고(identical distribute..

1. 자기상관함수(ACF) 1.1. 자기상관함수 자기상관(Auto Correlation)이란 시계열을 구성하는 확률변수들이 서로 상관되는 성질을 의미한다. 시계열의 자기상관을 측정할 때는 첫째, 시계열의 자기상관함수를 구하는 방법을 사용할 수 있다. 자기상관은 time lag k에 대하여 정의한다. 시계열 $X_{t}$의 k차 자기상관함수 ACF는 다음과 같다. $$\rho(k) = Corr(X_{t}, X_{t-k}) = \frac{Cov(X_{t}, X_{t-k})}{\sqrt{Var(X_{t})Var(X_{t-k})}}$$ 만약 시계열이 정상적이라면 $Var(Z_{t})= Var(Z_{t-k})$이 성립한다. 따라서 정상시계열의 자기상관함수는 $$\rho(k) = \frac{\gamma(k)}{\g..

1. 시계열의 차분 1.1. 차분 차분(differencing)이란 주어진 시계열의 변화분을 구하는 과정을 말한다. 예컨대 t번째 시계열이 $X_{t}$라고 할 때 차분 시계열 $Y_{t}$는 다음을 만족하는 시계열이다. $${\Delta}X_{t} = X_{t} - X_{t-1}$$ 가령 다음과 같은 분기별 시계열에 대하여 차분한 시계열은 아래와 같다. 차분을 수행하면 원 시계열의 첫번째 값은 포함하지 않는다. 차분의 시차: 차분이란 일반적으로 시차(time lag)가 1인 차분을 의미하지만 다양한 시차에 대하여 구해질 수 있다. 가령 시차가 2인 차분은 아래와 같다. $${\Delta}_{2}X_{t} = X_{t} - X_{t-2}$$ 차분을 거친 시계열을 한 번 더 차분하는 것을 2차 차분이라고 ..

1. 시계열의 개념1.1. 시계열의 정의 시간 t에 대해서 나타낸 확률변수의 수열 $X_{t}$를 시계열이라고 한다.$$\{X_{t}\} = {X_{1}, X_{2}, \cdots}$$ 1.2. 시계열의 특징하나의 대상을 지속적으로 관찰해 구성한 것이 시계열이기 때문에, 시계열을 구성하는 확률변수들은 서로에 대하여 독립적이지 못한 경우가 대부분이다. 예컨대 주가를 일별로 관측해 얻은 주가들은 서로에 대하여 상관을 갖는다. 이를 자기상관이라고 한다. 직전 주가를 가지고 다음날 주가가 예측 가능하다? 라는 것에 의문을 가질 수 있지만 통계학적으로 보았을 때 일별 주가가 독립이 아니라는 주장은 사실이다. 어느날 삼성전자의 주가가 6만원이라고 할 때 그 다음날 삼성전자의 주가가 6만 500원이나 5만 9500원..