이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크
Options, Futures, and Other Derivatives
ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021
www.pearson.com
이전 편 링크: 주요 방법론 개요
파생상품 가치평가 방법론 #3 주요 방법론 개요
이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 978013693
seungbeomdo.tistory.com
Numerical 방법 중 하나인 Binomial tree modeling
1. Model
Binomial Tree 방법에서
1) 만기까지의 기간 [0,T]는 n개의 구간 [0,Δt], [Δt,2Δt], ⋯, [(n−1)Δt,T]로 나누어진다.
2) 각 time step에서 기초자산은 u만큼 상승하거나, d만큼 하락한다.

위와 같은 방식으로 기초자산의 움직임을 모델링한다. 초기에 기초자산 가격이 S0이었다면, 그 다음 step에서는 p의 확률로 uS0가 되거나 1−p의 확률로 dS0이 된다. 그 다음에는 u2S0, udS0, 또는 d2S0가 된다.
2. Parameters
그렇다면 p, u, d의 값은 어떻게 정해야 할까? Binomial model을 공식화한 CRR(1979) 논문에서는 실제 기초자산 가격의 확률분포를 잘 나타내기 위하여 u와 d를 다음의 값으로 사용할 것을 제안하고 있다.
실제 기초자산 가격의 변동성이 σ일 때, u=eσ√Δt, d=e−σ√Δt
u와 d를 추정한 후 위험중립적 상승확률 p=a−du−d로 기초자산 가격이 상승한다고 가정한다.
이때 a는 위험중립적 세계에서 Δt 동안의 기초자산 가격의 기대상승률 e(r−q)Δt이다.
r은 무위험이자율, q는 자산수익률이다.
왜 위험중립적 상승확률 p가 저렇게 계산되는지는 이전 포스팅(https://seungbeomdo.tistory.com/37)을 참조
3. Risk-Neutral Valuation
이상의 모형에서 RNV로 파생상품의 가격을 구하려면 다음의 단계를 따르면 된다.
(1) 실제 기초자산 가격 움직임을 모델링할 만큼 충분히 작은 Δt에 대하여 Binomial tree를 완성한다.
(2) Tree의 마지막 step에서 만기 시점의 기초자산 가격들을 구한 후, 대응하는 파생상품의 payoff를 구한다.
(3) 각 payoff가 발생하는 위험중립적 상승확률에 따라 위험중립적 기대 payoff를 구한 후, 무위험이자율 r로 할인한다.
n개의 time step으로 파생상품의 잔존만기를 분할했을 때, 만기 시점에서 기초자산 가격은 n+1개 존재한다.
이 중 i번째 node에서 기초자산의 가격은 Sn,i=S0uidn−i, i=0,1,...,n
만기 시점 i번째 node에서의 payoff는 곧 파생상품의 가치 fn,i이다.
만기 시점에 i번째 node에 도달할 위험중립적 확률은 nCi∗pi(1−p)n−i
따라서 위험중립적으로 평가한 초기 파생상품의 가격은 f0=e−rTΣni=0nCi∗pi(1−p)n−ifn,i
4. Simulation
설명한 방법이 제대로 먹히는지 한번 구현해보자.
주가의 초기 가격이 100, 연간 변동성이 20%, 무위험이자율 5%일 때,
행사가격이 100이고 만기가 1년인 콜옵션의 가격을 구해보자.
S0 = 100
K = 100
sigma = 0.2
r = 0.05
T = 1
n = 5
u = np.exp(sigma*np.sqrt(T/n))
d = 1/u
a = np.exp(r*T/n)
p = (a-d)/(u-d)
ST = []
fT = []
PT = []
for i in np.arange(0,n+1):
v = S0 * u**i * d**(n-i)
ST.append(v)
payoff = np.maximum(v - K, 0)
fT.append(payoff)
prob = math.comb(n, i) * p**i * (1-p)**(n-i)
PT.append(prob)
df = pd.DataFrame({'Stock price':np.round(ST,3), 'payoff':np.round(fT,3), 'risk-neutral prob':np.round(PT,3)})
df
만기까지의 기간을 우선 n=5개의 interval로 분할할 때 만기 주가의 상태와
그에 대응하는 콜옵션의 payoff 및 risk-neutral probabaility는

각 payoff에 위험중립확률을 곱하여 무위험이자율로 할인하면 10.806 정도가 나온다.
잔존만기를 더 잘게 쪼개서(n을 키워서) 어떤 값으로 수렴하고 있는지 여부를 알아보자.
S0 = 100
K = 100
sigma = 0.2
r = 0.05
T = 1
F = []
for n in np.arange(1, 50):
u = np.exp(sigma*np.sqrt(T/n))
d = 1/u
a = np.exp(r*T/n)
p = (a-d)/(u-d)
ST = []
fT = []
PT = []
for i in np.arange(0,n+1):
v = S0 * u**i * d**(n-i)
ST.append(v)
payoff = np.maximum(v - K, 0)
fT.append(payoff)
prob = math.comb(n, i) * p**i * (1-p)**(n-i)
PT.append(prob)
f0 = np.exp(-r*T)*np.sum(np.array(fT)*np.array(PT))
F.append(f0)
def BSMcall(S, K, r, sigma, T):
d1 = (np.log(S/K) + (r + (sigma**2)/2)*T)/(sigma*np.sqrt(T))
d2 = d1 - sigma*np.sqrt(T)
call = S * norm.cdf(d1) - K * np.exp(-r*T) * norm.cdf(d2)
return call
plt.plot(np.arange(1, 50), F, label = 'Binomial model')
plt.axhline(BSMcall(S0, K, r, sigma, T), color = 'black', linestyle = '--', label = 'BSM')
plt.xlabel('n')
plt.ylabel('estimated call price')
plt.legend()
plt.show()

n이 1일 때부터 50일 때까지 각각 binomial model로 추정한 가격이 발산하지 않고 수렴하고 있음을 알 수 있다. 그리고 그 수렴값은 Black-Scholes-Merton Model의 가격이라는 것도 알 수 있다.
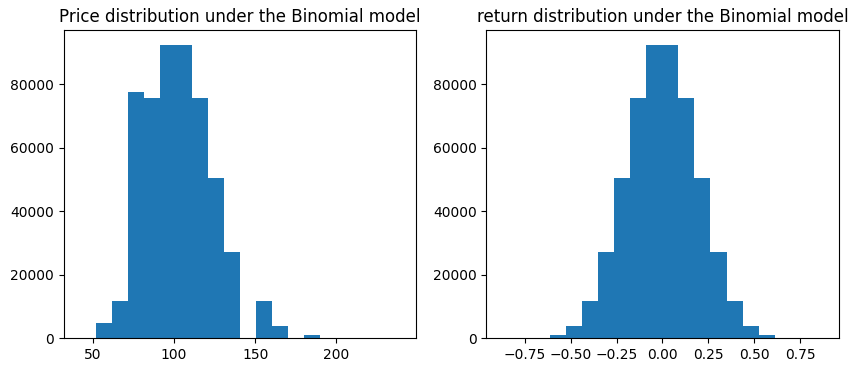
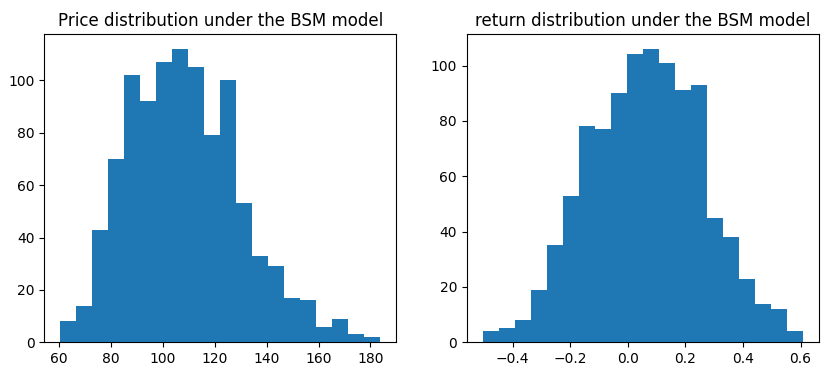
이 점은 어찌보면 당연하다. binomial model에서 만기까지의 기초자산 수익률은 이항분포를 따른다. 그런데 n의 값이 충분히 커지면 이항분포는 정규분포로 수렴한다. 만기까지의 수익률이 정규분포를 따른다는 것은 BSM 모형의 가정과 동일하다. 결국 n이 충분히 클 때 이항모형은 기초자산 수익률이 정규분포를 따를 때 옵션의 payoff를 위험중립적으로 평가한 것이며, 이는 BSM 모형과 완전히 동일하다.
아래는 n = 20일 때 이항모형 하에서의 확률분포와 BSM 모형에서의 확률분포를 비교한 것이다.
'파생상품&금융공학' 카테고리의 다른 글
| Delta Hedging과 ELS #1 ELS는 왜 사고 왜 팔까 (0) | 2024.01.20 |
|---|---|
| 파생상품 가치평가 방법론 #5 Binomial Tree (2) Backwardation method (0) | 2023.12.11 |
| 파생상품 가치평가 방법론 #3 주요 방법론 개요 (2) | 2023.12.03 |
| 파생상품 가치평가 방법론 #2 위험중립적 가치평가 (Risk-Neutral Valuation) (1) | 2023.12.03 |
| 파생상품 가치평가 방법론 #1 파생상품의 "공정한 가격" (3) | 2023.12.03 |