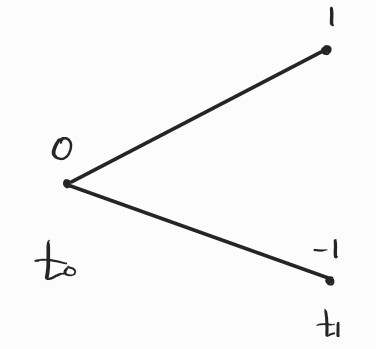
금융시장을 분석하는 텍스트를 읽다보면 자주 마주치는 것이 바로 주가의 Log-nomality라는 가정이다. 사실 이것은 현실의 주가의 성질을 가리키는 것은 아니고, 금융시장의 분석에서 익숙하게 사용되는 가정이라고 생각하면 된다. 그냥 편하게 로그노말이라고 이제 쓰겠다. 0. 주가의 확률분포우리의 관심은 주가가 특정 시점에 어떤 값을 갖느냐이다. 사실 그건 알 수가 없다. 미래에 관한 예측이기 때문이다. 하지만 우리가 특정 시점에 주가가 어떤 값을 가질지 확률분포를 알 수 있다는 것은 상대적으로 현실적인 아이디어이다. 이 포스트에서 다루고자 하는 것은 바로 주가의 확률분포를 구하는 과정인 것이고 그 중 자주 사용되는 분포가 바로 로그노말 분포이다. 1. 이항 모델주가는 오르거나 내린다. 가장 단순한 모형..