주가가 Log Normality를 갖는다는 것

 

금융시장을 분석하는 텍스트를 읽다보면 자주 마주치는 것이 바로 주가의 Log-nomality라는 가정이다. 사실 이것은 현실의 주가의 성질을 가리키는 것은 아니고, 금융시장의 분석에서 익숙하게 사용되는 가정이라고 생각하면 된다. 그냥 편하게 로그노말이라고 이제 쓰겠다.

 

0. 주가의 확률분포

우리의 관심은 주가가 특정 시점에 어떤 값을 갖느냐이다. 사실 그건 알 수가 없다. 미래에 관한 예측이기 때문이다. 하지만 우리가 특정 시점에 주가가 어떤 값을 가질지 확률분포를 알 수 있다는 것은 상대적으로 현실적인 아이디어이다.

 

이 포스트에서 다루고자 하는 것은 바로 주가의 확률분포를 구하는 과정인 것이고 그 중 자주 사용되는 분포가 바로 로그노말 분포이다.

 

1. 이항 모델

주가는 오르거나 내린다. 가장 단순한 모형으로 내일 주가가 오늘 주가보다 오르거나 내리는 둘 중 하나라고 생각해보자. 현재 주가가 S0일 때, p의 확률로 1만큼 오르고, 1-p의 확률로 1만큼 내린다고 생각하자.

.

 

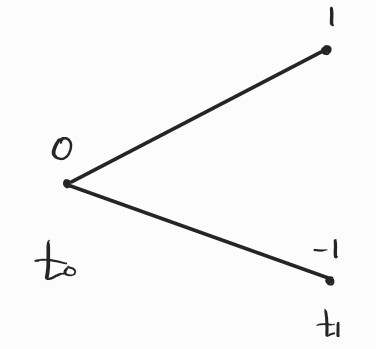
통계학 기초를 알고 있는 사람이라면 내일의 주가는 베르누이 분포를 따르게 된다는 것을 예측할 수 있다. 베르누이 분포란 베르누이 시행의 결과로 얻어지는 확률변수의 분포를 말한다. 베르누이 시행이란 확률변수의 결과가 A와 B 둘 중 하나로만 결정되는 확률실험을 말한다.

 

앞에서 주가의 변화분은 1가 되거나(A) -1이 되거나(B) 둘 중 하나라고 말했으므로 주가의 변화분은 베르누이 시행의 결과이고, 따라서 베르누이 분포를 따른다.

$\Delta S \sim Bernoulli(1,-1; p)$​

$E[\Delta S]=0$

$Var[\Delta S] = 2p$

​

하지만 내일의 주가는 단지 오늘의 주가에서 1원을 올리거나 1원을 내리거나 하는 식으로 단순하게 결정되지 않는다. 현실에 보다 가까운 모형을 다음과 같이 떠올려보자.

 

주가는 오늘과 내일 사이에 1원 오르거나 1원 내리지만, 한 번에 결정되는 것이 아니라 n번의 변화를 거치면서 최종적으로 결정된다고 하자. 즉 주가는 n번 움직이며, n번 동안의 주가의 변화분이 누적되어서 내일의 주가가 결정된다.

 

각각의 스텝에서 주가는 1원 오르거나 1원 내리거나 둘 중 하나이다. 따라서 최종적인 주가의 변화분은 n과 -n 사이의 n+1개의 정수 중 하나로 결정된다.

 

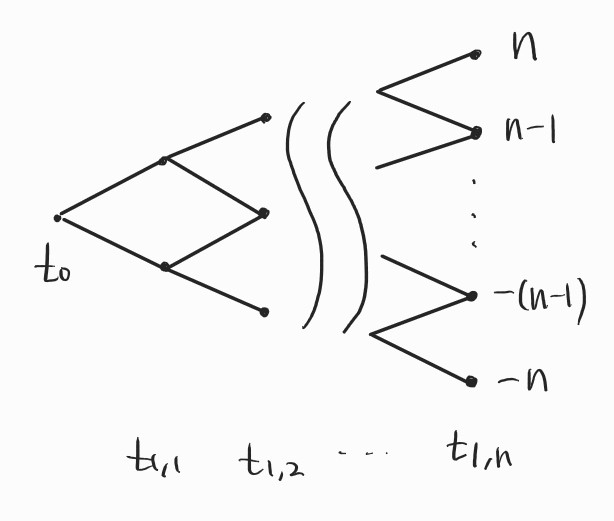
이는 주가의 누적 변화분이 이항 분포를 따른다는 것을 의미한다. 이항 분포란 베르누이 시행을 n번한 결과로 얻어지는 확률변수의 분포를 말한다. 우리가 지금 주가에 대해 하는 것은, 주가가 1원 오르거나 1원 내리는 시행을 n번 반복하면서 각 시행에서 얻어진 주가의 변화분을 누적하는 것이다. 즉 각각의 시행은 주가가 1원 오르거나 1원 내리는 베르누이 시행이다. n번의 베르누이 시행의 누적된 결과로 얻어지는 주가의 최종 변화분은 정확히 이항 분포를 따른다(이것을 랜덤워크 Random Walk라고도 말한다).

 

$\Delta S \sim Binomial(1,-1;n,p)$​

$E[\Delta S] = 0$​

$Var[\Delta S]=2np$

​

여기서 한 번 테크닉이 필요하다. 위의 경우에서 문제점이 무엇이냐면, 주가의 움직임 횟수 n이 많아지면 분산이 무한으로 발산한다는 것이다. 물론 무한한 시간 동안 주가가 변화한다면 최종적인 변화의 분산은 무한이 될 것이다. 하지만 우리의 경우에서는 무한한 시간을 보는 것이 아니고, 시간은 1일로 고정돼 있는 상태에서 1일이라는 시간을 무한하게 쪼개는 것이다. 우리는 단지 하루를 무한하게 쪼개서 거래를 했을 뿐인데, 하루의 마지막에 결정되는 주가가 무한한 범위를 갖는다는 것은 이상하다.

 

문제는 n번의 스텝에서 주가가 1씩 오르락 내리락한다고 하는 데 있다. 그러나 하루를 n번으로 쪼개어 생각하는 경우 각각의 쪼개진 스텝에서 주가의 변화분은 조금 더 작게 움직인다고 생각하는 것이 직관적이다. 따라서 우리는 각각의 스텝에서 주가가 1씩 오르락 내리락한다고 하지 않고, (1/n)^(1/2), 즉 1/n의 제곱근씩 오르락 내리락한다고 할 것이다. 왜 1/n이 아니라 1/n의 제곱근으로 하냐면 후자의 결과가 우리의 현실과 더 부합하기 때문이다.

 

$\Delta S\ \sim \ Binomial\left(\frac{1}{\sqrt{n}},-\frac{1}{\sqrt{n}};\ n,\ p\right)$​

$E\left[\Delta S\right]\ =\ 0$​

$Var\left(\Delta S\right)\ =\ 2p$

​

각 스텝에서 주가의 변화를 n의 제곱근으로 나누기로 했을 때, 최종적인 주가 변화분의 분산은 처음의 베르누이 분포의 그것과 동일하다. 우리가 주가의 변화를 n번으로 쪼개어 생각하는 것은 현실에서 하루 동안 주가가 여러번 변화하는 것을 반영하기 위함이다. 동시에 주가가 일정한 범위 내에서 결정된다는 것도 유지되어야 한다. 이를 위해서 하루를 n개의 스텝으로 쪼개고, 각각의 스텝에서 주가의 변화분을 n의 제곱근만큼으로 나누었더니, 수학적으로 바람직한 모형이 만들어졌다(이것을 Scaled Random Walk라고도 말한다).

 

2. 이항 모델의 극한

지금까지 본 것은 주가의 누적 변화분이 이항 분포를 따른다는 것이었다. 여기서 현실에 한발짝 더 가까워지기 위해 다음과 같은 간단한 사고실험을 해보자.

 

우리는 오늘부터 내일까지 시간을 n으로 나누고 n번의 주가 변화가 하루 동안 발생한다고 가정했다. 그런데 실제로 시간은 연속적이다. 이 말은 주가가 오늘부터 내일까지 무수히 많은 베르누이 시행을 거친다는 이야기이다. 따라서 최종적인 주가의 누적 변화분은 n이 무수히 많을 때의 이항분포를 따른다고 할 수 있다.

 

이항분포에서 n이 충분히 큰 수로 갈 때, 이항분포에는 어떤 변화가 생길까? 놀랍게도, 이때 이항분포는 정규분포로 근사하게 된다(중심극한정리). 그리고 이때의 평균과 분산은 이항분포의 그것과 동일하다. 이를 확인하기 위해 n이 10일 때와 100일 때, 그리고 10000일 때의 이항분포를 그려보았다. 이항분포의 모수 p는 0.5로 모두 동일하다.

 

 

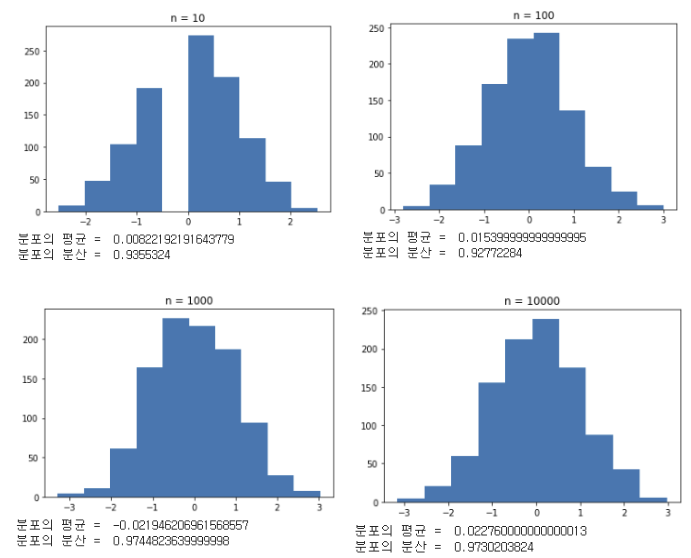
n이 커질수록 분포의 형태가 정규분포로 가까워짐을 알 수 있다. 또한 각각의 경우에서 이론적인 평균은 모두 0이며, 분산은 모두 1이다. 이론적인 예측과 실험의 결과가 근사적으로 동일하다.

 

이러한 사실을 사용해서 우리는 오늘과 내일 사이의 주가의 변화분(n번의 주가 변화분의 누적)은 근사적으로 정규분포를 따른다고 말한다. (근사적으로 따르는 것이므로 아래의 식이 정확한 것은 아니다)

 

$\Delta S\ \sim \ N\left(0,\ 2p\right)$

​

3. 주가의 로그노말 분포

일반적으로 주가의 확률과정은 다음과 같은 확률미분방정식(SDE)으로 나타낸다.

 

$\Delta S\ =\ \mu \cdot \Delta t\ +\ \sigma \cdot \Delta W\cdot \Delta t$​

$where\ \mu \ =\ drift\ rate,\ \sigma ^2\ =\ variance,\ $​

$and\ \Delta W\ \sim \ N\left(0,1\right)$

​

여기서 잠시, 주가의 변화분은 현재 주가 수준이 얼마나 되느냐에 비례한다. 즉 1000원짜리 주가의 변화분보다는 100000원짜리 주가의 변화분이 더 크다. 따라서 우리는 위 식을 조금 수정하여

 

$\Delta S\ =\ \mu \cdot S\cdot \Delta t\ +\ \sigma \cdot S\cdot \Delta W\cdot \Delta t$

​

라고 두고, 양변을 S로 나누어 다음의 식을 얻는다.

 

$\frac{\Delta S}{S}\ =\ \mu \cdot \Delta t\ +\ \sigma \cdot \Delta W\cdot \Delta t$

​

우리의 단순한 모형에서는 다음과 같이 보다 간략한 SDE로 나타난다.

 

$\frac{\Delta S}{S}\ =\ \sigma \cdot \Delta W\cdot \Delta t$​

$where\ \mu \ =\ 0,\ \sigma ^2\ =\ 2p\ and\ \Delta W\ \sim \ N\left(0,1\right)$

​

이는 사실

 

$\frac{\Delta S}{S}\ \sim \ N\left(0,\ 2p\cdot \Delta t^2\right)$

​

과 같은 의미이며, 우리의 경우에서 시간 증가분($\Delta t$) = 1이므로 앞서 적은 주가 변화분의 노말분포 근사식과 같다. 단 주가 변화분이 주가 수준에 비례한다는 것을 반영하기 위해 분모에 S를 추가한 점만이 다르다.

 

한편 관심의 대상이 되는 시간 변화를 1일이 아니라 2일, 10일 등등으로 하려면 $\Delta t$의 값을 바꿔주면 된다. 우리가 지금까지 시간 변화 기간을 1일이라고 가정한 것은 일종의 표준 확률 과정을 얻기 위함이었다고 생각하면 된다.

 

마지막으로, 많은 논문들에서 모델링에 사용하는 주가수익률은 로그수익률이다. 로그수익률은 주가수익률과 수치적으로 매우 유사하면서, 동시에 수학적으로 다루기가 매우 편리한 성질이 있다. 로그수익률이 주가수익률과 수치적으로 매우 유사하다는 것은 로그함수의 성질과 테일러 전개식을 가지고 보일 수 있다.

 

$\left(1\right)\ \ln \left(1+x\right)\approx x\ \ for\ a\ sufficiently\ small\ x$​

$\because \ \ln \left(1+x\right)\ \approx \ \ln \left(1+0\right)\ +\frac{1}{1+0}\left(x-0\right)$​

$\left(2\right)\ \ln \left(\frac{S_{t+1}}{S_t}\right)\ =\ \ln \left(\frac{S_t+\Delta S}{S_t}\right)\ =\ \ln \left(1\ +\ \frac{\Delta S}{S_t}\right)\ \approx \frac{\Delta S}{S_t}$

​​​

따라서, 우리의 SDE는 다음과 같이 바뀐다.

 

$\ln \left(\frac{S_{t+1}}{S_t}\right)\ =\ln \left(S_{t+1}\right)-\ln \left(S_t\right)=\ \sigma \cdot \Delta W\cdot \Delta t$

​

정리하면

 

$\ln \left(S_{t+1}\right)=\ln \left(S_t\right)+\sigma \cdot \Delta W\cdot \Delta t$

​

이는 정규분포를 따르는 확률변수(우변의 두번째 항)에 $ln(S_t)$라는 상수를 더해준 것뿐이다. $S_t$는 현재 주가이므로, 현재 시점에서 상수이다. 따라서

 

$\ln \left(S_{t+1}\right)\sim N\left(\ln \left(S_t\right),\ \sigma ^2\cdot \Delta t^2\right)$

​

이는 내일 주가에 로그를 취한 것이 정규분포를 따른다는 사실을 의미한다. 어떤 확률변수에 로그를 취한 값이 정규분포를 따른다면, 그 확률변수는 로그노말 분포를 따른다고 말한다. 그러므로 주가는 로그노말 분포를 따른다. 이게 서두에서 밝힌 주가의 로그노말 분포이다.

 

4. 현실의 주가 분포

주가의 로그노말 분포라는 것은 그냥저냥 쓰는 가정은 아니다. 그냥 세상 모든 것들이 노말 분포를 따르니까 주가도 노말 분포를 따르겠지 라는 생각으로 쓰는 가정은 아니라는 것이다.

 

이 포스트에서 쭉 썼듯이, 주가가 위 아니면 아래로 움직이는 이항 모델을 생각하고, 이항 모델의 타임 스텝을 무한하게 쪼개서 연속적인 시간 동안의 거래를 모델에 반영했다. 그리고 그 결과로 주가의 로그노말 분포를 얻었다.

 

이는 사실 현실 그 자체를 반영한다. 현실에서도 주어진 시점의 주가는 위 아니면 아래로 움직인다. 주가가 1원씩 움직이지 않고 2원씩 움직이기도 한다고? 2원씩 움직이는 것을 더 쪼개서 1원씩 두번 움직였다고 생각하면 된다. 주가가 위 아니면 아래로 움직이지 않고 횡보하기도 한다고? 처음에는 위 아니면 아래로 한 번 갔다가 다시 반대로 움직인 것이라고 마찬가지로 쪼개어 생각하면 그만이다.

 

그렇다면 현실의 주가는 실제로 로그노말 분포를 보일까? 애석하게도 꼭 그렇다고 말할 수는 없다.

 

논의에서 암묵적으로 사용한 가정이 있었는데 매 타임스텝에서 첫번째는 주가는 서로 독립적으로 움직인다는 가정이다. 즉 이전 스텝에서 주가가 올랐는지 내렸는지는 다음 스텝에서 주가가 오르는지 내리는지에 영향을 주지 않는다는 가정이다.

 

하지만 실제 주가의 움직임은 바로 직전의 주가 움직임에 큰 영향을 받으며, 바로 다음 주가의 움직임에 큰 영향을 준다. 한번 탄력을 받아 오르기 시작하는 주가는 계속 오르고, 한번 꺾인 주가는 계속 내리는 것을 우리는 잘 알고 있다. 그리고 장기적인 관점에서 보면, 높은 주가는 언젠가는 떨어지고 낮은 주가는 언젠가는 오른다는 것도 알고 있다. 이러한 주가의 성질을 시계열적 상관이라고 얘기하는데, 하여간 독립이 아니라는 뜻이다.

 

베르누이 시행의 결과를 누적한 것이 이항 분포가 되려면 각각의 베르누이 시행이 독립적이어야 한다. 그러나 주가를 가지고 하는 베르누이 시행은 독립적이지 않으므로 그 누적이 이항 분포로 되지 않는다. 이항 분포가 아니므로 시간을 무한하게 쪼개어도 정규 분포로 가지 않는다.

 

두번째로 우리가 사용한 암묵적인 가정은 분포의 평균과 분산이 변화하지 않는다는 것이다. 그러나 거시경제 상황이나 기업 고유의 상황에 따라서 주가의 분포 자체가 계속 흔들릴 수 있다. 주가 분포의 평균이 변화할 수도 있고, 분산이 변화할 수도 있다. 그러면 실제 주가의 분포는 여러개의 분포가 중첩된 상태로 나타날 것이고 뭐라 말하기 어려운 꼴의 분포가 나타나는 것이다.