이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크
Options, Futures, and Other Derivatives
ISBN-13: 9780136939979 Options, Futures, and Other Derivatives Published 2021
www.pearson.com
3편
파생상품 이론 #3 선물을 활용한 헷징 전략
이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 978013693
seungbeomdo.tistory.com
1. 이자율의 복리 계산
1.1. 복리 주기(Compounding Frequency)
1.1.1. 복리 주기의 정의
- 어떤 예금상품의 이자율이 연 x%라고 할 때, 그 실제 수익률이 첫 인상과는 다른 경우가 많다. 그 이유 중에 하나는 이자율이 어떤 복리 주기로 계산됐는지, 즉 연 복리인지 반년 복리인지, ... 등에 따라 수익률이 달라진다는 데 있다.
- 복리 주기란 이자율이 적용되는 주기를 말한다. 가령 이자율이 연 10%일 때 연간 복리(Annual Compounding)이면 초기 투자된 원금 $100에 대하여 1번의 10% 이자율이 붙는다. 따라서 1년 후의 원금은
$$ 100 * (1 + 0.1) = 110 $$
- 동일하게 이자율이 연 10%일 때 분기 복리(Quarterly Compounding)이면 원금에 대하여 분기마다 4번의 이자율이 붙는다. 따라서 1년 후의 원금은
$$ 100 * (1 + \frac{0.1}{4})^{4} = 110.38 $$
- 이처럼 복리 주기가 얼마인지에 따라 실제 수익률은 달라지게 된다.
- 일반적인 표현으로, 연간 m번의 복리가 발생한다고 할 때, 원금 A를 투자하면 n년 후 원리금은 아래와 같다.
$$ A (1 + \frac{R}{m})^{nm} $$
1.1.2. 상이한 복리 주기 이자율 간 상등관계
- 또한 서로 다른 복리 주기를 가진 이자율 간의 상등관계(Equivalent Rate)를 구할 수도 있다. $R_{1}$은 연간 $m_{1}$번의 복리로 계산된 이자율이고 $R_{2}$는 연간 $m_{2}$번의 복리로 계산된 이자율이라고 하자. 이때 두 이자율이 상등하다는 것은 두 경우 만기 원리금이 동일하다는 것을 말한다. 따라서
$$ A (1 + \frac{R_{1}}{m_{1}})^{nm_{1}} = A (1 + \frac{R_{2}}{m_{2}})^{nm_{2}} $$
$$R_{2} = m_{2} [(1 + \frac{R_{1}}{m_{1}})^{\frac{m_1}{m_2}} - 1] $$
1.2. 연속복리(Continuous Compounding)
- 연속복리란 주어진 기간 동안 복리가 연속적으로 발생하는 경우를 말한다. 즉 위의 복리 계산 식에서 m이 무한대로 갈 때의 그것을 의미한다. 연속복리를 통해 구해진 원리금은 지수함수의 형태로 나타난다.
$$ {\lim}_{m \to \infty} A(1+\frac{R}{m})^{nm} = Ae^{Rn} $$
- 연속복리와 상등인 경우의 이자율을 구하는 것도, 만기 시의 원리금을 동일하게 하는 조건을 대입하면 쉽다. 연속복리 이자율이 $R_{c}$이고, m번 복리 이자율이 $R_{m}$일 때 두 이자율이 상등하다면
$$ A(1+\frac{R_{m}}{m})^{nm} = Ae^{R_{c}n}, $$
$$R_{m} = m(e^{\frac{R_{c}}{m}} - 1)$$
and
$$R_{c} = m*ln(1 + \frac{R_{m}}{m})$$
2. 이자율의 종류
금리를 수반한 거래에서 인용되는 이자율의 대표적인 유형들을 알아보자.
2.1. 국채 금리
- 국채 금리란 정부가 자국 통화 표시로 발행한 채권의 금리를 말한다.
- 일반적으로 정부가 자국 통화 표시 채권에 대하여 디폴트할 가능성은 없기 때문에 무위험 채권의 현실적인 대용치로 쓰인다.
2.2. 오버나이트 금리(OIS Rate)
- 은행 간에 거래되는 1일 만기물 채권의 금리를 말한다.
- 시중은행들은 매일 법정 지급준비금을 중앙은행에 예치해야 한다. 그런데 매일 은행들이 항상 필요한 만큼의 예치금을 가지고 있는 것은 아니므로 초과 지급준비를 보유한 은행들이 지급준비가 부족한 은행들에게 1일 만기로 필요한 만큼을 대출을 해준다.
- 이러한 거래에 적용되는 금리를 오버나이트 금리라고 하며, 우량한 제도권 은행들이 참여하는 채권 거래이므로 신용이 높은 채권이다.
2.3. 환매조건부(Repo) 채권 금리
- 환매조건부 거래에서 책정되는 금리를 말한다.
- 환매조건부 거래란 차입자가 증권을 발행하고 이 증권을 일정 기간 후 가산된 금액으로 재매수(환매)하겠다고 약정하는 거래를 말한다. 재매수 시에 가산되는 금액만큼이 금리의 역할을 하고 이를 Repo 금리라고 부른다.
- 만약 차입자가 만기에 환매 의무를 이행하지 않을 시 대부자는 보유한 증권을 유동화하면 되므로, 담보부 채무 거래라고도 이해할 수 있다.
2.4. LIBOR
- LIBOR(London Interbank Offered Rate)란 우량한 글로벌 은행들이 서로에 대해 어느정도의 금리로 대차거래가 가능한지 설문조사를 통해 책정되는 일종의 지수(Index)이다.
- 역사적으로 LIBOR는 다양한 금융거래에서 기초가 되는 금리로 사용되었다.
- 설문대상인 은행들이 서로 짜고 치는 사건이 발생해서 현재는 더이상 사용되지 않는다.
2.5. 무이표채 금리(Zero Rate)
- 무이표채 금리는 위에서 다룬 금리들처럼 제도적이라기보다는 개념적인 것을 의미한다.
- 무이표채란 만기 시에만 원리금 지급이 발생하고 중도에는 이자 지급이 발생하지 않는 채권을 말하며, 이 채권에서 계산된 금리가 무이표채 금리이다.
- 대부분의 채권들은 무이표채가 아니다. 일반적으로 반년마다 이자를 지급하다가 만기에 원금을 포함한 이자를 지급하는 방식이다.
- 무이표채 금리가 중요한 이유는 금융자산의 가격을 평가하는 데 필수적으로 사용되기 때문이다. 금융자산의 가격은 그 자산을 보유함으로써 발생하는 미래의 모든 현금흐름들의 현재가치 합이다. 이때 각각의 현금흐름들을 현재가치로 바꿔오기 위해서는 할인율이 필요하다.
- 할인율은 시장에서 거래되는 채권 금리를 준용하는데, 딱 그 시점에서 발생하는 현금흐름만을 지급하는 채권의 금리를 구하기 위해서는 무이표채 금리를 사용해야 한다.
3. 채권 가치 평가
3.1. 채권의 가격 결정 원리
- 채권의 이론적인 가격은 채권을 보유함으로써 발생하는 미래 현금흐름들의 현재가치 합이다.
- 이때 각 현금흐름들의 현재가치를 구하기 위해서 앞서 밝힌 바와 같이 무이표채 금리를 사용한다. 각 시점에서 무이표채 금리가 $R_{t}$, 이표 $C_{t}$일 때 채권의 가격 $B$는
$$ B = {\Sigma}_{t=1}^{N} C_{t} * e^{-R_{t} * t} $$
- 가령, 2년 만기 채권이 있고 원금은 100달러이다. 연 이자율을 6%이고 반년마다 지급된다. 6개월, 1년, 1년 6개월, 그리고 2년 만기인 무이표채 금리가 연속복리 기준으로 각각 5%, 5.8%, 6.4%, 6.8%라고 하자. 이때 채권의 가격은
$$ 3e^{-0.05*0.5} + 3e^{-0.058*1.0} + 3e^{-0.064*1.5} + 103e^{-0.068*2.0)} = 98.39 $$
3.2. 채권의 수익률(Yield)
- 채권의 수익률이란, 채권의 시장가격과 채권의 현금흐름 현재가치 합이 일치하도록 하는 단일 할인율을 말한다. 즉 채권 수익률 $y$에 대하여 다음의 식이 성립한다.
$$ B = {\Sigma}_{t=1}^{N} C_{t} * e^{-y*t} $$
- 가령, 앞에서 구한 채권의 수익률을 구하자면, 다음의 식을 만족하는 수익률 $y$가 될 것이다.
$$ 3e^{-y*0.5} + 3e^{-y*1.0} + 3e^{-y*1.5} + 103e^{-y*2.0)} = 98.39 $$
$$ \therefore y = 6.76% $$
3.3. 액면가 수익률(Par Yield)
- 액면가 수익률이란 채권의 가격을 채권의 액면과 일치시키도록 하는 이표율을 말한다.
- 채권의 액면이 A일 때, 액면가 수익률은 다음을 만족하는 매기 동일한 이표 금액 C를 채권의 액면으로 나눈 것이다.
$$ B = {\Sigma}_{t=1}^{N} C * e^{-R_{t} * t} $$
4. 무이표채 금리 구하기
일반적으로 시장에서 거래되는 채권들은 무이표채가 아니기 때문에, 시장에서 곧바로 무이표채 금리를 구할 수는 없다. 무이표채 금리를 구하기 위한 테크닉인 부트스트랩 방법(Bootstrap Method)을 알아보도록 하자.
4.1. 부트스트랩 방법
- 부트스트랩 방법이란 시장에서 가장 짧은 만기의 무이표채 금리를 먼저 구한 후, 이를 토대로 긴 만기의 무이표채 금리를 순차적으로 구해나가는 방법이다. 예시를 들어서 이해하는 것이 가장 빠르다.
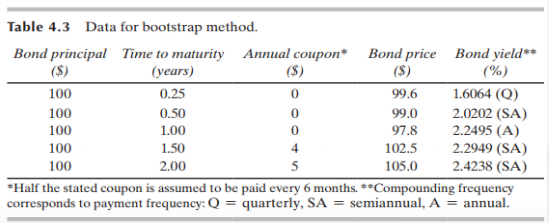
- 첫 3행에 등장하는 채권들은 중도 이자 지급이 존재하지 않는 순수한 할인채이다. 따라서 우리는 3번째 행까지의 채권 가격으로부터 연속복리를 가정한 1분기, 반년, 그리고 1년 만기의 무이표채 금리들을 각각 구할 수 있다.
$$ 100 = 99.6 * e^{R_{0.25} * 0.25} \therefore R_{0.25} = 1.603% $$
$$ 100 = 99.0 * e^{R_{0.5} * 0.5} \therefore R_{0.25} = 2.010% $$
$$ 100 = 97.8 * e^{R_{1} * 1} \therefore R_{1} = 2.225% $$
- 4번째 행에 등장하는 1년 반 만기를 가진 채권은 반년마다 $2씩(연 $4씩) 중도 이자 지급이 발생하므로 무이표채가 아니다. 이 경우에 무이표채 금리를 구하기 위하여, 먼저 1년 반 만기의 채권 가격은 매 기의 현금흐름들의 현재가치 합으로 결정되었다고 가정한다. 그리고 우리는 반년과 1년 만기의 무이표채 금리를 알고 있으므로 남은 미지수는 1년 반 만기의 무이표채 금리뿐이다.
$$ 102.5 = 2 * e^{-R_{0.5} * 0.5} + 2 * e^{-R_{1} * 1} + 102 * e^{-R_{1.5} * 1.5} $$
$$ 102.5 = 2 * e^{-0.02010 * 0.5} + 2 * e^{-0.02225 * 1} + 102 * e^{-R_{1.5} * 1.5} $$
$$ \therefore R_{1.5} = 2.284% $$
4.2. 보간법(Interpolation) .
- 시장에서 모든 개별 시점을 만기로 가지는 채권 데이터를 구할 수는 없다. 따라서 데이터를 구할 수 없는 만기의 무이표채 금리는 그 시점의 전후에서 구할 수 있는 두 무이표채 금리를 보간하여 구한다.
- 가령 부트스트랩 방법을 통해 두 무이표채 금리를 구했고 하나는 만기가 1년, 다른 하나는 만기가 2년이라고 하자. 1년 만기 무이표채 금리는 1.5%, 2년 만기 무이표채 금리는 1.9%이다. 이로부터 1.75년 만기의 무이표채 금리를 구하려면 앞에서 구한 두 금리 사이를 3:1로 내분하는 지점의 값인 1.8%이다.
- 전술한 방법은 선형보간법이라고 하며, 만기에 대해 금리가 선형적으로 증가한다는 가정 하에서 사용된다. 비선형적인 증가를 가정한 방법도 물론 있다.
4.3. 수익률 곡선(Yield Curve)
- 수익률을 만기에 대하여 표시한 그래프를 수익률 곡선이라고 한다. 무이표채 수익률의 그것은 Zero curve라고도 부른다. 앞에서 부트스트랩 방법과 선형보간법을 적용해 얻은 수익률 곡선은 아래와 같다.
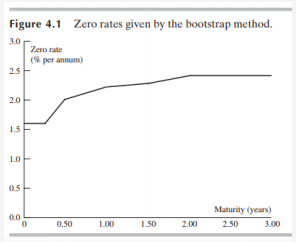
5. 선도 금리(Forward Rates)
5.1. 선도 금리
5.1.1. 선도 금리의 정의
- 선도 금리란 미래 특정 기간 동안에 적용되는 무이표채 금리를 말한다. 가령 1년 만기 무이표채 금리가 현재로부터 1년 간의 차입 거래에 적용되는 이자율이라면, 1년 후 시점에서 1년 동안 적용되는 무이표채 금리는 선도 금리라고 말한다.
- 현물 이자율이 주어져있는 경우, 선도 금리를 구하는 것은 간단하다. 예를 들어 1년 간의 무이표채 금리가 3%이고 2년 간의 무이표채 금리가 4%라고 하자. 이때 1년 후 시점에서 1년 동안 적용되는 무이표채 금리 즉 선도 금리는 4%이다. 왜냐하면 2년 동안 4% 금리를 받는 것과, 1년 동안 3% 금리를 받고 재투자하여 5% 금리를 1년 동안 받는 것이 동일한 결과를 주기 때문이다.
$$ e^{0.03*1} * e^{R_{f} * 1} = e^{0.04 * 2} $$
$$ \therefore R_{f} = 0.05 $$
- 일반적으로 표현하면 다음과 같다. $T_{2}$년 동안 적용되는 금리가 $R_{2}$이고, $T_{1}$년 동안 적용되는 금리가 $R_{1}$일 때, $T_{1}$년 후 시점에서 $T_{2} - T_{1}$년 동안 적용될 선도 금리 $R_{f}$는
$$ R_{f} = \frac{R_{2}T_{2} - R_{1}T_{1}}{T_{2} - T{1}} $$
단, $T_{2} > T_{1}$이고, 연속복리를 가정한다.
- 이는 다음과 같이 다시 쓸 수 있다.
$$ R_{f} = R_{2} + (R_{2} - R_{1})\frac{T_{1}}{T_{2}-T_{1}} $$
- 만약 수익률곡선이 $T_{1}$과 $T_{2}$ 사이에서 양의 기울기를 갖는다면 $R_{2} > R_{1}$이므로 선도금리는 $R_{2}$보다 높아야 할 것이다.
5.1.2. 순간 선도 금리
- $T_{2}$가 $T_{1}$에 극한적으로 가까워졌다고 생각하면, 이때의 선도금리를 순간 선도 금리(Instantaneous Forward Rate)라고 말한다.
$$ R_{f} = R + T\frac{\partial {R}}{\partial {T}} $$
5.2. FRA(선도금리계약; Forward Rates Agreements)
5.2.1. FRA의 정의
- FRA란 고정된 선도금리와 변동금리를 교환하기로 하는 계약이다. FRA 매수자는 선도금리로 약정된 만큼의 고정금리를 지급하고, 미래 시점에서 실제 금리를 수취한다.
- 일반적으로 FRA에서 원금은 포지션의 크기를 나타낼 뿐 실제 원금을 교환하지는 않는다. 다만 약정한 선도금리와 실제금리 간의 차액만을 교환할 뿐이다.
- 가령, 2022년 1월에 FRA를 체결하는데 2023년 1월 초부터 4월 초까지의 선도금리가 3%라고 하자. 그리고 실제 2023년 1월 초에 실현된 3개월물 금리는 3.5%라고 하자. 원금은 100만 달러라고 하자. 이때 FRA의 매수포지션은
$$1,000,000 * (0.035 - 0.030) * 0.25 = 125,000$$
만큼을 수취한다.
- 일반적으로 FRA는 금리가 확정되는 시점에서 차액을 교환한다. 따라서 차액의 현재가치만큼을 교환한다. 위의 예시를 들면 12만 5천 달러는 2023년 4월 초를 기준으로 하는 가치이므로 $125,000 * e^{-0.035 * 0.25} = 123,911$만큼을 2023년 1월 초에 교환한다.
5.2.2. FRA의 가치 평가
- FRA의 가치는 약정한 선도금리와 평가 시점의 선도금리의 차이로 인해 변화한다. 계약 시점에서 약정 금리는 선도금리로 하는 것이 일반적이므로, 계약 시점에서 FRA의 가치는 0이 된다.
5.2.3. FRA의 활용
- 선도거래가 현물포지션에 대한 헷지 수단으로 쓰이듯, FRA도 채권의 현물포지션에 대한 헤지 수단으로 쓰인다. 예를 들어 향후 6개월 후 3개월 동안 변동금리를 수취하기로 한 투자자는 6개월 후 3개월물 금리의 불확실성에 직면한다. 이때 6개월 FRA의 매도 포지션을 취할 경우 현재의 선도금리로 본인이 수취할 금리를 고정시키는 효과를 얻게 된다.
6. 듀레이션과 볼록성
6.1. 듀레이션(Duration)
6.1.1. 듀레이션의 정의
- 듀레이션은 채권의 보유자가 채권의 투자금액(채권 가격)을 회수하는 데 걸리는 기간을 나타낸다.
- 무이표채의 경우, 만기에만 지급이 발생하므로, 듀레이션은 곧 만기와 동일하다.
- 이표채의 경우, 만기 이전에도 지급이 발생하므로, 듀레이션은 만기보다는 작다.
- 듀레이션은 다음과 같이 정의된다. 각 시점 $t_{i}$에서의 현금흐름이 $c_{i}$이고 수익률이 $y$이면
$$ D = \frac{\Sigma_{i=1}^{N} t_{i} c_{i} e^{-yt_{i}}}{B} $$
$$ D = \Sigma_{i=1}^{N} t_{i} \frac{c_{i}e^{-yt_{i}}}{B} $$
- 따라서 듀레이션은 각 현금지급이 발생하는 시기들의 가중평균이라고 할 수 있다. 이때 가중치는 각 현금지급이 채권 가격에서 차지하는 비중을 의미한다.
6.1.2. 채권가격의 민감도 분석
- 채권 수익률이 변화할 때, 채권가격의 변화는 다음의 식으로 근사할 수 있다.
$$ \Delta B = \frac{dB}{dy} \Delta y $$
- 채권의 가격은 현금흐름의 현재가치 합이므로, 채권가격의 수익률에 대한 미분은 아래와 같이 구한다.
$$ B = \Sigma_{i=1}^{N} c_{i}e^{-yt_{i}} $$
$$ \frac{dB}{dy} = \Sigma_{i=1}^{N} c_{i} e^{-yt_{i}}(-t_{i}) = -DB $$
- 따라서, 수익률이 변화할 때 채권가격의 변화는 듀레이션으로 간략하게 나타낼 수 있다.
$$ \frac{\Delta B}{B} = -D \Delta y $$
- 다음 예시로부터, 채권가격은 현재 94.213이고, 듀레이션은 2.653이다. 수익률이 0.1% 증가한다면, 새로운 채권가격은 $94.213 - 2.653 * 0.001 = 93.963$이 된다.

6.1.3. 수정 듀레이션(Modified Duration)
- 앞서 논의한 듀레이션은 이자율이 연속복리로 발생한다는 가정 하에 구한 것이다. 보다 일반적인 표현으로, 연간 m번의 복리가 발생하는 경우의 듀레이션은 다음의 수정 듀레이션 $D^{*}$이 상대적으로 더 정확하다.
$$ D^{*} = \frac{D}{1+y/m} $$
6.2. 포트폴리오 듀레이션(Portfolio duration)
- 채권 포트폴리오 전체의 듀레이션은 포트폴리오를 구성하는 개별 채권들의 듀레이션의 가중평균으로 구할 수 있다. 이때 가중치는 개별 채권의 가격이 포트폴리오 전체 가격에서 차지하는 비중이라고 하는 것이 직관적이다.
- 단 채권 포트폴리오 전체의 가격 변화를 듀레이션으로 분석할 때 모든 채권의 수익률이 동일하게 변화한다고 가정한다는 데 유의해야 한다.
- 포트폴리오를 구성하는 각 채권들은 만기가 모두 상이하므로 수익률도 모두 다르다. 그런데도 수익률이 동일하게 변화한다는 것은 수익률의 변화가 항상 수익률 곡선 자체의 평행 이동에만 기인한다고 가정하는 것이다. 현실에서는 수익률 곡선의 기울기가 변화하기도 하므로 이는 다소 강한 가정이다.
6.3. 볼록성(Convexity)
- 수익률이 변화함에 따라 채권의 듀레이션도 계속 변화한다. 따라서 듀레이션 분석은 작은 수익률 변화에 대해서만 근사적인 결과를 줄 뿐 큰 수익률 변화에 대해서는 부정확한 결과로 이어진다.

- 수익률 변화에 대하여 듀레이션, 즉 채권 가격의 민감도도 변화하는 것은 채권의 볼록성이라는 개념으로 포착한다. 볼록성 $C$는 다음과 같이 정의된다.
$$ C = \frac{1}{B} \frac{d^{2}B}{dy^{2}} = \frac{\Sigma_{i=1}^{N} c_{i}t_{i}^{2}exp(-yt_{i})}{B} $$
- 채권의 볼록성을 가격 변화 분석에 활용하기 위하여, 테일러 전개를 통해 채권 가격을 다음과 같이 근사시키자.
$$B = B(y_{0}) + \frac{dB}{dy}|_{y=y_{0}}({y-y_{0}}) + \frac{1}{2}\frac{d^{2}B}{dy^{2}}|_{y=y_{0}}({y-y_{0}})^2$$
$y_{0}$은 현재의 수익률을 나타낸다.
- 따라서 채권 가격의 변화는 아래와 같다.
$$\Delta{B} = \frac{dB}{dy}\Delta{y} + \frac{1}{2}\frac{d^{2}B}{dy^{2}}(\Delta{y})^2$$
$$\frac{\Delta{B}}{B}= -D\Delta{y} + \frac{1}{2}C(\Delta{y})^2$$
- 채권 가격의 듀레이션과 볼록성을 계산하여, 채권 투자자는 채권에 대한 포지션을 헷지하기 위한 여러가지 전략의 기초로 사용할 수 있다.
7. 수익률의 기간 구조 이론
7.1. 수익률의 기간 구조(Term Structure)
- 수익률의 기간 구조란, 만기에 대하여 수익률이 보이는 특정한 패턴을 의미한다. 주로 수익률이 만기에 대하여 증가하는 것을 의미한다.
7.2. 유동성 선호 이론
- 이를 설명하기 위한 대표적인 이론은 유동성 선호 이론(Liquidity Preference Theory)이다. 유동성 선호 이론에 따르면, 만기에 대하여 수익률이 상수일 때 투자자들은 짧은 만기로 투자를 하고 이를 rolling하는 것을 원한다. 왜냐하면 어차피 결과적인 수익률은 동일한데 굳이 투자금액을 오래 묶어둘 필요가 없기 때문이다.
- 동시에 차입자들은 긴 만기로 차입하기를 원한다. 고정된 금리로 오랜 기간 차입을 유지하면서 금리 변화의 위험을 회피하고자 하기 때문이다.
- 따라서 이자율이 만기에 대하여 일정하다면, 긴 만기의 대출에 대한 수요가 공급보다 많기 때문에 긴 만기의 대출금리가 상승한다.
- 이는 일반적으로 우상향 수익률 곡선이 관측되는 것과도 일치하는 이론적 예측이다.
'파생상품&금융공학' 카테고리의 다른 글
| 파생상품 이론 #6 스왑 (0) | 2023.02.07 |
|---|---|
| 파생상품 이론 #5 선물 가격 결정 이론 (2) | 2023.02.03 |
| 파생상품 이론 #3 선물을 활용한 헷징 전략 (7) | 2023.01.19 |
| 파생상품 이론 #2 선물시장의 이해 (0) | 2023.01.18 |
| Black-Scholes-Merton Model #3: BSM 모델의 검증(Python 예제) (1) | 2023.01.15 |