이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크
Options, Futures, and Other Derivatives
ISBN-13: 9780136939979 Options, Futures, and Other Derivatives Published 2021
www.pearson.com
2편
파생상품 이론 #2 선물시장의 이해
이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 978013693
seungbeomdo.tistory.com
1. 헷징의 기본 원리
1.1. 매도 헷지(Short Hedges)
- 매도 헷지: 미래 시점에 현물 매도를 수행해야 하는 거래자가 사용하는 헷지로서 선물의 숏 포지션을 수반한다.
- 예시) 원유 생산자가 3개월 후에 원유 생산이 완성될 것으로 보고 미리 매도 가격을 확정하고 싶어하는 상황이다. 원유 선물 3개월물의 가격이 50달러일 때 매도 포지션을 체결했다고 하자.
- 만약 3개월 후 현물 가격이 55달러이면
- 원유를 현물시장에서 55달러에 매도
- 보유한 선물 숏포지션을 청산하기 위해 55달러 지급하므로 50 - 55 = 5달러 손실
- 원유의 유효가격(effective price)는 50달러 = 최초 체결한 선물가격과 동일
- 만약 3개월 후 현물 가격이 47달러이면
- 원유를 현물시장에서 47달러에 매도
- 보유한 선물 숏포지션을 청산하기 위해 47달러 지급하므로 50 - 47 = 3달러 이득
- 원유의 유효가격은 50달러 = 최초 체결한 선물가격과 동일
- 어느 경우에건 최초 체결한 선물가격인 50달러로 원유를 매도한 결과를 얻게 된다. 즉 이 기업은 3개월 후에 원유를 배럴당 50달러에 매도할 것으로 확정된다.
- 이때 만기에 현물시장과 선물시장에서 두 번의 거래를 수행하는 것에 의문이 들 수 있다. 선물 매도 포지션을 체결했다면 선물 만기에 약정한 가격으로 매도하면 동일한 결과를 얻을텐데, 뭐하러 번거롭게 (1) 현물시장에서 팔고, (2) 선물시장에서 포지션을 따로 종결하는 두 개의 거래를 거쳐야 할까?
- 선물은 기초자산을 인도(delivery)하는 것이 가능한 계약이지만, 실제로 인도가 이루어지는 경우는 거의 없다. 선물 계약에 정해진 대로 인도를 수행하는 것의 행정적 번거로움이 더 크기 때문이다.
- 따라서 대부분의 헷저들은 현물은 현물시장에서 곧바로 거래하고, 선물 포지션을 따로 청산함으로써 '결과적인' 헷지 효과를 얻고자 한다.
1.2. 매수 헷지(Long Hedges)
- 매수 헷지: 미래 시점에 현물 매수를 수행해야 하는 거래자가 사용하는 헷지로서 선물의 롱 포지션을 수반한다.
- 예시) 미국 수출기업이 수출 대금을 6개월 후에 한국 원화로 수취하게 되어 달러 표시 대금의 가치를 미리 확정하고 싶어하는 상황(대금을 원화로 받아주는 착한 기업)이다. 달러 선물 6개월물의 가격이 1000원일 때 매수 포지션을 체결했다고 하자.
- 만약 6개월 후 현물 환율이 1200원이면
- 수취한 수입대금으로 달러를 현물시장에서 1200원에 매수
- 보유한 선물 롱포지션을 청산하면서 1200원 수취하므로 1200 - 1000 = 200원 이득
- 달러의 유효가격(effective price)는 1000원 = 최초 체결한 선물가격과 동일
- 만약 6개월 후 현물 가격이 950원이면
- 수취한 수입대금으로 원유를 현물시장에서 950원에 매수
- 보유한 선물 롱포지션을 청산하면서 950원을 수취하므로 950 - 1000 = 50원 손실
- 달러의 유효가격은 1000원 = 최초 체결한 선물가격과 동일
- 어느 경우에건 최초 체결한 선물가격인 1000원으로 달러를 매수한 것과 동일한 결과이다. 만약 이 기업의 수출대금이 1억원이었다면 6개월 후에 10만 달러의 대금을 받게 될 것으로 확정할 수 있다.
- 이때 만기에 현물시장과 선물시장에서 두 번의 거래를 수행하는 이유는 위에서 설명했다.
2. 베이시스 위험
2.1. 베이시스(Basis)
- 베이시스란 주어진 시점에서 현물가격과 선물가격의 차이로 정의된다. Bt=St−Ft
- 동일한 기초자산을 공유하지만, 현물가격과 선물가격이 항상 동일한 속도로 변화하는 것은 아니므로, 만기 이전에 베이시스의 값은 일정하지 않은 움직임을 보인다. 물론 만기에는 이론적으로 베이시스가 0이 되어야 한다.
2.2. 베이시스 위험(Basis Risk)
- 숏 헤지를 취한 경우를 생각해보자. 전술한 바와 같이 만기에 헷저가 수취하는 유효가격은
- 롱 헤지를 취한 경우를 생각해보자. 만기에 헷저가 지불하는 유효가격은
- 이때 헷지 시작 시점인 0시점의 선물 가격 F0는 0시점에서 알려져있지만, 만기에 발생할 베이시스 BT의 값은 확률변수이다. 따라서 만기에 실제 손익을 결정할 수 없는 위험이 발생하고 이를 베이시스 위험이라고 한다.
- 물론 앞에서 만기에는 항상 베이시스가 0이 된다고 했다. 그러한 이상적인 경우에는 헷지 만기 시점에서 항상 선물가격이 헷저가 직면하는 유효가격이 될 것이다. 하지만 베이시스가 만기에 0이 되지 않는 경우는 현실에서도 종종 발생하며, 헷저가 꼭 선물만기까지 포지션을 유지하지 않고 중도에 청산할 수도 있다.
2.3. 선물 만기의 선택
- 헷저가 의도하는 헷징 종료 시점과 거래소에서 거래되는 선물의 만기가 일치하지 않는 경우는 흔하다. 예컨대 주식 포트폴리오를 보유한 투자자가 4월에 포트폴리오를 매도하고 시장을 떠나고자 하는데, 코스피 주가지수 선물의 만기는 3, 6, 9, 12월에만 존재한다. 따라서 헷징을 종료하려는 시점(4월)과 이용 가능한 선물 만기가 일치하지 않는다. 이럴 때는 어떻게 해야할까?
- 첫째, 헷징 종료 시점보다 만기가 늦게 끝나는 선물을 선택한다. 왜냐하면 실제로 인도가 발생하게 되면 피곤하기 때문이다.
- 둘째, 헷징 종료 시점의 현물 가격과 (그 시점이 만기가 아닌)선물 가격은 일치하지 않는다. 즉 베이시스가 제로가 되지 않는다. 그리고 베이시스는 만기로부터 멀리 떨어질 수록 커질 가능성이 크다. 따라서 헷징 종료 시점과 가장 가까운 만기를 선택한다.
- 결론적으로, 헷징 종료 시점보다 늦으면서도 가장 가까운 만기의 선물계약을 선택한다.
3. 교차 헷징
3.1. 교차 헷징(Cross Hedging)
- 헷징 만기 불일치와 함께 헷징의 또다른 이슈는 현물과 동일한 기초자산을 사용하는 선물 계약이 존재하지 않을 수도 있다는 것이다. 예컨대 항공사는 비행기 연료로 제트유(jet oil)를 사용하지만 제트유의 선물 시장이 충분한 유동성을 가지고 형성되지 않을 수 있다. 이 경우에는 제트유와 유사한 자산인 원유(crude oil)의 선물을 사용하는 대안을 고려할 수 있다. 이러한 헷징을 교차 헷징이라고 부른다.
- 헷지 비율(Hedge ratio): 교차 헷징을 사용할 경우, 현물 포지션의 손익과 선물 포지션의 손익이 완벽하게 동조되지 않기 때문에 현물 포지션과 선물 포지션을 1대1로 매칭하는 것이 최적이라는 보장이 없다. 따라서 현물포지션 당 얼마의 선물포지션을 가지고 있을 것인지, 즉 헷지 비율을 결정하는 것이 중요한 문제가 된다.
3.2. 최소분산 헷지비율(Minimum Variance Hedge Ratio)
- 최적의 헷지비율은 헷저의 포지션 가치의 변동을 최소화하는 헷지 비율이라는 것을 직관적으로 이해할 수 있다. 헷지 비율을 h라고 하면, 1개의 현물 계약에 대해 h개의 선물 계약을 보유하는 셈이므로 헷저의 포지션은
- 따라서 헷저의 포지션 변화는
- 헷저의 포지션 변화의 분산을 구하면
- 분산을 최소화하는 헷지비율 h를 결정하기 위해 위 식을 h에 대해 편미분하여 얻은 1계 조건은
- 이때 최적 헷지비율 h*는 현물가격 변화를 선물가격 변화에 OLS 회귀시켜 얻은 직선의 기울기 계수라는 것을 확인할 수 있다. 따라서 현물가격 변화와 선물가격 변화의 과거 데이터로부터 최적 헷지비율을 추정하여 사용한다.
3.3. 최적의 계약 수
- 일반적으로 선물계약은 1계약당 복수의 거래단위를 정하고 있다. 따라서 최적의 헷지비율을 반영한 최적 계약 수 N*는 다음과 같다. QA는 헷지 대상 포지션의 크기(거래단위 수)이고 QF는 선물 1계약의 거래단위 수이다.
- 한편 선물거래는 일일정산 시스템에서 운영된다. 따라서 선물헷지는 만기까지 하나의 선물 포지션을 보유하는 것이 아니라 매일매일 새로운 선물 포지션을 갈아끼우는 것이라고 이해해야 한다. σS와 σF를 현물가격과 선물가격의 일별변화율(ex. dS/S)의 표준편차라고 정의하면 새로운 최적 계약의 수
where
and
4. 주가지수 선물
4.1. 주가지수 선물
- 주가지수 선물은 주가지수를 기초자산으로 하는 선물계약을 말한다.
- 주가지수라는 기초자산은 만기에도 인도가 불가능하므로, 주가지수 선물 거래는 만기에 차액만을 결제한다.
4.2. 주가지수 선물을 활용한 포트폴리오 헷징
- 주가지수 선물을 활용해 투자자가 보유한 포트폴리오를 헷지할 경우, 최적의 계약 수는 앞서 설명한 것과 유사하게 결정된다.
- 눈치챘겠지만 여기서 베타는 CAPM 모델에서의 베타이다. 즉 포트폴리오의 초과수익률을 시장 초과수익률에 대하여 OLS 회귀시켜 얻은 직선의 기울기 계수이다.
4.3. 포트폴리오의 베타를 조정하기
- 주가지수 선물을 베타의 비율로 매도할 경우, 선물계약을 포함한 전체 포트폴리오의 베타는 제로가 된다. 기존 포트폴리오의 베타는 주가지수 변화에 대한 민감도를 의미하는데, 딱 그만큼을 숏 때림으로써 주가지수 변화에 대한 민감도를 완전하게 상쇄시켰기 때문이다.
- 물론 이 경우에, 주가지수가 아니라 주가지수 '선물'의 숏 포지션을 취했다는 것에 유념해야 한다. 주가지수와 주가지수의 선물이 동일한 것은 아니기 때문에, 선물을 활용해 헷지했을 때 주가지수 자체에 대한 민감도를 헷지했다는 주장은 약간은 비약일 수 있다.
- 그러면 포트폴리오의 베타를 제로가 아니라 어떤 임의의 값으로 바꾸어보는 것은 어떨까? 이 경우에도 주가지수 선물을 적절히 활용하면 된다. 만약 현재 포트폴리오의 베타가 β일 때, 이를 β∗로 바꾸고자 한다면, 필요한 선물계약의 수는
- 이 값이 음수라면 선물 숏, 양수라면 선물 롱 포지션이 필요하다는 뜻이다.
5. 선물 만기 연장하기(Stack and Roll)
- 헷저가 원하는 헷징 종료 시점과 시장에서 이용 가능한 선물의 만기가 일치하지 않는 문제를 앞에서 다루었다. 이 경우 헷징 종료 시점보다 늦으면서 동시에 가장 가까운 선물 만기를 택하면 된다고 했었다.
- 그런데 모든 이용 가능한 선물 만기가 헷징 종료 시점보다 빠르면 어떨까? 예컨대 1년 후에 들어오는 수출 대금을 원화 가치로 확정하고 싶은데, 1년 만기의 달러화 선물 혹은 원화 선물은 원하는 만큼 유동성이 풍부하지 않을 가능성이 높다. 이 경우 선물의 만기를 실질적으로 연장하는 테크닉이 있다.
- 먼저 유동성이 풍부한 3개월 만기의 달러 선물을 숏한다. 그리고 이 선물의 만기가 도래했을 때 포지션을 청산하고 그 다음 3개월물의 달러를 숏한다. 그리고 이 과정을 1년 동안 반복하면 매 시점마다 3개월 선물을 사용하는 것이므로 유동성을 편안하게 활용할 수 있고 동시에 선물 만기가 늘어나는 효과를 가질 수 있다. 이 과정을 "Stack and Roll"이라고 한다.
- 예시를 들어서 이해해보자.
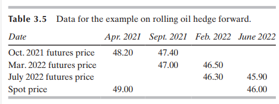
- 2021년 4월 시점에서 한 회사는 2022년 6월에 생산 완료될 예정인 원유의 매도가격을 확정하고 싶어한다. 그러나 2022년 6월에 만기가 도래하는 원유 선물은 유동성이 적어서 원하는 만큼 숏을 칠 수가 없다.
- 우선 현물가격은 현재 배럴당 49달러이다.
- 회사는 2021년 10월 만기의 원유 선물을 숏친다. 이때 선물가격은 48.20달러이다.
- 2021년 9월에, 10월 만기 선물가격은 47.40달러가 되었다. 보유한 원유 선물을 청산하면 0.8달러 이득을 본다. 동시에 2022년 3월 만기 선물을 47달러에 숏친다.
- 2022년 2월에, 3월 만기 선물가격은 46.50달러가 되었다. 보유한 원유 선물을 청산하면 0.5달러 이득을 본다. 동시에 2022년 7월 만기 선물을 46.3달러에 숏친다.
- 2022년 6월에, 7월 만기 선물가격은 45.9달러가 되었다. 보유한 원유 선물을 청산하면 0.4달러 이득을 본다. 그리고 이 시점에서는 원유 생산이 완료되었으므로 헷징을 종료하고 원유를 판다. 원유 현물가격은 46달러가 되었으므로 46달러를 얻는다.
- 그럼 이 회사가 원유를 판매해 얻은 유효가격은 현물시장에서 6월에 얻은 46달러와, 선물을 갈아탈 때마다 발생했던 차익들(0.8 + 0.5 + 0.4 = 1.7)의 합인 47.7달러가 된다. 만약 이 회사가 원하는 선물계약이 없다고 손 놓고 있었으면 2022년 6월 현물가격인 46달러만 받을 수 있었을 것이다.
'파생상품&금융공학' 카테고리의 다른 글
| 파생상품 이론 #5 선물 가격 결정 이론 (2) | 2023.02.03 |
|---|---|
| 파생상품 이론 #4 이자율 (0) | 2023.01.29 |
| 파생상품 이론 #2 선물시장의 이해 (0) | 2023.01.18 |
| Black-Scholes-Merton Model #3: BSM 모델의 검증(Python 예제) (1) | 2023.01.15 |
| 파생상품 이론 #1 파생상품의 정의와 시장 구조 (0) | 2023.01.15 |