2편: BSM 모델을 사용한 옵션 가격의 해석적 해 도출
Black-Scholes-Merton Model #2: 옵션 가격의 해석적 해(Analytic Solution)
1편: 파생상품 가격 이론의 의의 Black-Scholes-Merton Model #1: 파생상품 가격 이론의 의의 1. 옵션의 정의 옵션의 정의를 짚고 넘어가자. 옵션이란 기초가 되는 자산(기초자산)을 사전에 약정된 가격(행
seungbeomdo.tistory.com
4. BSM 모델의 검증
옵션가격에 대한 BSM 모델이 잘 들어맞는지 확인하기 위해 데이터로 실습을 해본다.
- 2022년 9월 만기인 행사가격 320의 코스피200 콜옵션 가격 데이터를 사용했다. KRX 한국거래소의 정보데이터시스템으로부터 2022년 6월 29일부터 9월 8일(해당 옵션의 만기일)까지의 콜옵션 가격의 종가를 구할 수 있다.
KRX 정보데이터시스템
증권·파생상품의 시장정보(Marketdata), 공매도정보, 투자분석정보(SMILE) 등 한국거래소의 정보데이터를 통합하여 제공 서비스
data.krx.co.kr
- 옵션의 가격을 구하기 위해서 BSM 모델에서 사용하는 독립변수는 기초자산의 가격, 행사가격, 무위험이자율, 잔존만기, 그리고 기초자산 수익률의 변동성이다.
- 기초자산(코스피200) 가격과 행사가격, 잔존만기는 옵션 데이터로부터 이미 확정돼있다.
- 무위험이자율은 통상적으로 91일물 CD금리를 사용한다.
- 변동성은 GARCH 모형 등 시계열 모형을 통해 추정한 값을 사용한다. 여기서는 적당한 값 0.15를 대입하자.
- BSM 모형의 해석적 해를 함수로 구현하자.
- 무위험이자율은 %단위이므로 100으로 나누어 실수값을 취하도록 한다. 또한 BSM 모형에서 사용하는 무위험이자율은 연속적으로 쪼개어진 거래 간격에서의 무위험이자율이다. 현실에서는 1일 단위로 거래가 이루어진다는 가정 하에 1거래일당 무위험이자율을 구하기 위하여 대략적인 연중 거래일 수인 250으로 나누어준다.
- 변동성도 무위험이자율과 마찬가지 이유로 1거래일 간의 변동성으로 바꾸어주어야 한다. BSM 모델이 가정하는 랜덤워크 하에서 변동성은 시간에 대하여 그 제곱근으로 증가한다. 따라서 연간 변동성이 데이터에서 주어질 경우 거래일 수의 제곱근으로 연간 변동성을 나누어주면 1거래일 간 변동성을 얻을 수 있다.
def bs_call(s, r, t, sig = 0.15, k = 320):
r = r/250/100
sig = sig/np.sqrt(250)
d1 = (np.log(s/k) + (r+(sig**2)/2)*t)/(sig*np.sqrt(t))
d2 = (np.log(s/k) + (r-(sig**2)/2)*t)/(sig*np.sqrt(t))
call = s*stats.norm.cdf(d1) - k*np.exp(-r*t)*stats.norm.cdf(d2)
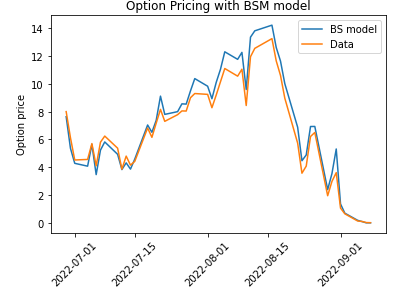
return call- BSM 모델을 가지고 예측한 옵션 가격과 실제 옵션 가격은 아래와 같다.
- 대략적으로 잘 맞는다는 것을 알 수 있다.
- 주어진 예측값의 평균제곱오차(MSE)는 0.557 정도가 나온다. 변동성을 무턱대고 가정하고 추정한 값이므로, 시계열 예측 모형 등을 근거로 추정된 변동성을 사용할 경우 오차를 좀더 줄일 수 있을 것이다.
'파생상품&금융공학' 카테고리의 다른 글
| 파생상품 이론 #3 선물을 활용한 헷징 전략 (7) | 2023.01.19 |
|---|---|
| 파생상품 이론 #2 선물시장의 이해 (0) | 2023.01.18 |
| 파생상품 이론 #1 파생상품의 정의와 시장 구조 (0) | 2023.01.15 |
| Black-Scholes-Merton Model #2: 옵션 가격의 해석적 해(Analytic Solution) (2) | 2023.01.10 |
| Black-Scholes-Merton Model #1: 파생상품 가격 이론의 의의 (0) | 2023.01.06 |