1. Computer Vision
- Computer Vision(CV) 문제는 컴퓨터가 이미지를 잘 이해할 수 있도록 하는 과제를 말한다.
- 가령 자율주행 자동차가 지금 앞에 있는 것이 사람인지 텅 빈 도로인지를 잘 파악할 수 있도록 하는 문제이다.
- 모든 CV에서 공통되는 단계는 주어진 이미지를 컴퓨터가 이해할 수 있는 방식으로 변환하는 것이다. 아래 그림에서 기차가 무너진 사진을 보면, 사람은 그냥 곧바로 기차가 무너졌다라고 인식한다. 하지만 컴퓨터에게 이 이미지를 입력하기 위해서는 이미지의 각 픽셀값으로 변환해서 주어야 한다.
- 이때 픽셀값은 흑백 여부를 나타내는 binary한 값일 수도 있고,
- 컬러 이미지라면 RGB가 조합된 벡터값이 될 것이다.

- CV를 어렵게 만드는 문제는 무엇이냐 하면, 일단 이미지를 보고 이게 기차인지 버스인지를 알려주는 것은 쉬운데, 이미지가 조금만 달라져도 컴퓨터가 인식을 제대로 못한다는 것이다. 예를 들어
- 컴퓨터가 학습한 기차가 검은색 기차였다면, 빨간색 기차는 기차로 인식을 못할 수 있다.
- 컴퓨터가 정면에서 바라본 기차를 학습했다면, 기차의 옆모습이나 뒷모습을 보고는 기차라고 인식하지 못할 수 있다.
- 기차가 지나가는 나무에 가려져서 기차 꼬리만 보인다든가 하면 기차라고 인식하지 못할 수 있다.
- 밝은 날에 촬영한 기차 사진은 잘 인식하지만, 어두운 밤에 지나가는 기차는 인식하지 못할 수 있다.
- 따라서 CV에서 가장 중요한 과제는 컴퓨터가 인식하고자 하는 이미지의 아주아주 본질적이고 고유한 특성을 찾는 일이다. 그런 본질적인 특성을 컴퓨터가 학습해두었다면, 기차가 옆모습이건 앞모습이건, 빨간색이건 무지개색이건 문제 없이 기차는 기차라고 인식할 것이다.
- 이 단계의 문제를 특성 추출, Feature Extraction이라고 한다. 특성 추출에 가장 효과적이라고 알려진 것은 딥러닝 뉴럴넷의 한 종류인 CNN이다.
2. CNN의 골격
2.1. Convolutional Layer와 FC Layer
- CNN은 크게 두 단계로 구성된다. 첫 단계는 이미지의 특성을 추출하는 Filter이고, 두번째 단계는 추출된 특성을 기반으로 이미지가 어느 범주에 속하는지 구분하는 FC Layer(Fully Connected Layer)이다.

- 이때 Filter 레이어는 Convolutional 레이어로 구체화된다. 그래서 CNN(Convolutional Layer)이다. 컨볼루션 레이어에서는 여러가지 연산을 통해 특성을 추출하는데, 특성을 추출하는 레이어들도 결국 하나의 뉴럴넷이다. 컨볼루션 레이어가 특성을 추출했을 때, 결과적으로 전체 뉴럴넷의 성능이 좋아지는 방향으로 컨볼루션 레이어의 파라미터들을 훈련한다.
- FC 레이어는 컨볼루션 레이어가 넘겨준 특성을 바탕으로 이미지를 분류하는 뉴럴넷이다. 이미지 분류의 성능이 좋아지는 방향으로 FC 레이어의 파라미터들을 훈련한다. 그냥 직전 포스팅에서 배운 뉴럴넷이랑 똑같다.
- 이때 FC 레이어라고 불리는 이유는, 뉴럴넷을 구성하는 모든 레이어의 뉴런들이 각각 서로 완전하게 연결되어있기 때문이다. 컨볼루션 레이어는 그렇지 않기 때문에 이와 구분해서 FC 레이어라고 부른다.
- FC 레이어는 직전 포스팅에서 다룬 기본적인 뉴럴넷과 다를 게 없기 때문에, 새로운 내용인 컨볼루션 레이어만 다룬다.
2.2. 합성곱(컨볼루션)
- 그럼 대체 합성곱이라는 게 무엇일까? 수학적인 정의는 이렇다. 두 함수 f와 g에 대해서 다음의 연산을 합성곱이라고 정의한다.
- 직관적으로 설명하면, 함수 f를 고정시킨 상태에서 함수 g를 t만큼 이동시키며 그 결과를 곱해 누적한 것이다. 사실 별로 직관적이지는 않다. 다만 이것은 합성곱의 수학적 정의이고, 다음 내용들은 따라가면서 왜 저렇게 정의했는지 감을 얻어보자.
- CNN에서 컨볼루션은 이미지의 특성을 추출하는 기법이라고 했다. 그 특성을 어떻게 추출하는지를 보자. 먼저 아래와 같이 주어진 이미지가 픽셀들의 집합으로 표현되었다고 하자.

- 3차원 직사각형의 가로와 세로는 픽셀의 가로 위치와 세로 위치를 나타내고, 두께(channel)는 RGB를 나타내는 축이다. 3차원 직사각형의 각 셀에는 그에 해당하는 픽셀값이 들어간다.
- 만약 이미지의 (1,1) 픽셀이 완전 새빨간색이라고 하자. 그럼 위 직사각형에서 (1,1,1)은 255가 되고, (1,1,2)와 (1,1,3)은 둘 다 0이 될 것이다.
- 컨볼루션이란 이 직육면체를 주어진 필터가 통과하면서 직육면체를 구성하는 셀값들의 가중치합을 뽑아내는 과정이다. 이래도 사실 이해가 가지는 않을 것이다. 예시 필터가 다음과 같다고 하자. 이 필터는 다음과 같이 생겼다. 필터의 각 셀의 값은 가중치를 의미한다.

- 그리고 이 필터를 다음의 직육면체에 통과시킨다. 근데 다음 그림은 직육면체는 아니다. 이해를 쉽게 하기 위해서 직육면체의 앞면만 가지고 진행하는 것인데, 실제 이미지는 직육면체로 표현되므로 이게 전부라고 생각하면 안 된다.

- 음영 처리된 부분은 지금 전체 이미지 중에서 해당 부분이 필터링되고 있다는 뜻이다. 필터링은 가중치합을 뽑아내는 것이라고 했는데, 저 부분에서 뽑아지는 값은
2*1 + 0*1 + 1*3 + 0*0 + 1*1 + 2*2 + 1*3 + 0*0 + 2*1 = 15가 된다.
- 그리고 이 15를 필터링된 값을 필터링으로 얻어지는 새로운 직육면체(특성맵; Feature map)에 저장한다.

- 다음으로 필터를 옆으로 민다. 여기서는 필터가 두 칸씩 옆으로 이동한다고 가정한다(몇 칸씩 이동해야되는지는 나중에 다룬다). 이동한 곳에서 또 가중치합을 뽑아 저장한다. 이번에는 17이 나왔다.

- 이 과정을 반복하면서 최종적인 특성맵의 셀을 다 채운다. 이게 컨볼루션이다. 앞에서 함수가 이동하면서 다른 함수에 곱한 것을 누적했다고 했는데, 바로 이런 의미에서 CNN은 이미지를 컨볼루션한다고 말하는 것이다.
3. 컨볼루션 레이어의 기본 요소
3.1. 커널(Kernel)
- 커널이란 위에서 말한 필터와 같은 의미이다. 그냥 주어진 무엇인가에 적용하는 함수라고 생각하면 편하다. 우리의 커널은 특성을 뽑기 위해 이미지에 적용되는 가중치합 함수이다.
- 커널은 가로*세로*채널의 사이즈를 가지고 있다. 커널의 가로*세로 사이즈는 전체 이미지의 사이즈보다 크지만 않으면 된다. 커널의 채널은 전체 이미지의 채널과 동일해야 한다.
- 커널의 각 셀은 가중치를 나타내며, 이 가중치들을 나중에 뉴럴넷으로 훈련한다.
- 커널은 한 이미지에 여러개를 사용할 수도 있다. 커널이 k개라면 추출된 특성이 담기는 특성맵의 채널이 k개가 된다. 즉 먼저 적용한 커널에서 얻어진 특성들을 특성 직육면체의 맨 앞에 깔아준다. 그 다음에 적용한 커널에서 얻어진 특성들은 특성 직육면체의 그 뒤 채널에 깔아주고, ... , 반복한다.
3.2. 스트라이드(Stride)
- 스트라이드란 커널이 움직이는 간격을 말한다. 1칸씩 움직일수도 있고, 2칸씩 움직일수도 있다. 아래 커널은 2칸씩 움직이면서 특성을 추출하므로 스트라이드가 2이다.
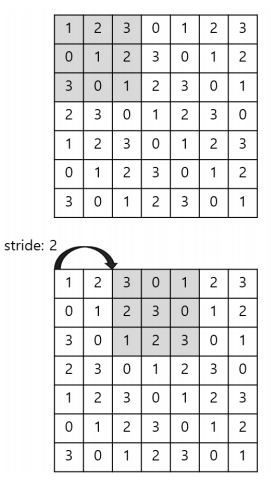
- 하지만 그 간격은 주어진 이미지와 커널 사이즈를 고려해서 딱 맞게 맞춰줘야 한다.
- 위의 이미지는 7*7(채널은 일단 무시하고) 사이즈인데 커널 사이즈는 3*3이므로 스트라이드가 3씩 이동할 경우 이미지 전체를 딱 맞게 훑지를 못한다. 이런 경우가 생기면 안 된다는 뜻이다.
- 스트라이드가 작으면 커널이 조금씩 이동하면서 많은 특성들을 찍어내므로 특성맵의 차원이 커질 것이고, 스트라이드가 커지면 커널이 성큼성큼 이동하면서 적은 특성들을 찍어내므로 특성맵의 차원이 작아질 것이다.
3.3. 패딩(Padding)
- 패딩이란 컨볼루션이 되는 이미지맵을 지정된 값들로 둘러주는 것을 말한다. 일반적으로는 제로 패딩(Zero padding)이라고 해서, 이미지맵의 주변을 0으로 둘러준다.
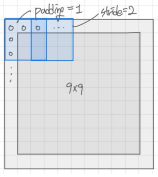
- 패딩을 해주는 이유는 첫째, 컨볼루션의 결과로 나온 특성맵의 차원이 인풋 이미지맵에 비해서 너무 빠르게 작아지는 것을 막기 위함이다. 특성맵의 차원이 너무 빠르게 줄어들면, 모델이 학습할 수 있는 특성의 개수가 빠르게 줄어든다는 것을 의미하므로 학습 효과가 줄어들 수 있다.
- 커널을 거쳤을 때 차원이 전혀 줄어들지 않도록 하는 패딩의 사이즈는 (필터 사이즈 - 1) / 2 이다.
- 둘째, 컨볼루션을 하게 되면 커널이 여러번 겹치는 영역, 주로 이미지의 가운데 영역들이 특성맵에서 과잉 대표된다. 이미지의 모서리에 위치한 영역들도 특성맵에 골고루 반영되도록 하기 위해서는, 이미지 사이즈를 확대시켜서 원래는 모서리에 위치해있던 영역들이 가운데로 이동하도록 하는 과정이 필요하다. 이 작업을 해주는 것이 패딩이다.
3.4. 특성맵의 사이즈
- 인풋 이미지는 앞서 살펴보았듯이 가로, 세로, 채널을 가진 3차원 직육면체이고 k개의 커널을 거쳐서 나온 특성맵은 채널이 k인 3차원 직육면체이다. 즉 채널의 크기는 커널의 개수에 의해서 고정된다.
- 특성맵의 2차원 사이즈는 다음과 같다. 원 이미지의 사이즈가 N, 커널 사이즈가 F, 패딩 사이즈가 P, 스트라이드가 S일 때, 특성맵의 2차원 사이즈는
3.5. Pooling Layer
- 풀링 레이어는 컨볼루션을 하지 않고 이전 레이어의 값의 일부만을 취하는 레이어를 말한다. 가령 이전 레이어에서 주어진 특성맵에서, 풀링 커널의 사이즈에 해당하는 각 영역의 최대값만 추출한다든지, 평균값을 구해 하나의 값으로 차원을 축소한다든지 하는 것이다.
- 풀링 기법은 모델이 학습하는 특성의 수가 너무 많을 때 과대적합을 막기 위해 차원 축소를 해주는 것으로 이해할 수 있다.
- 아래 그림은 최대값만 뽑는 max pooling의 예시이다. 보통 풀링이라고 하면 맥스 풀링을 의미한다.
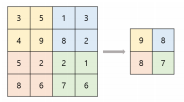
- 또한 풀링은 컨볼루션 레이어가 모두 끝난 후에 FC 레이어로 넘겨주기 이전에 3차원의 특성맵을 1차원의 벡터로 줄여주는 데에도 사용한다. 뉴럴넷의 인풋 벡터는 1차원의 벡터이기 때문에 이 작업이 필요하다.
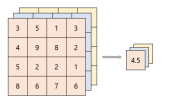
- 이때 자주 사용하는 풀링은 Global Average Pooling이다. 이는 특성맵을 구성하는 각 채널에서 평균값을 뽑아, 채널당 하나의 평균값만이 존재하도록 결과를 반환한다. 그러므로 원래 특성맵의 차원이 (가로, 세로, 채널)이었다면 Global Average Pooling을 거친 벡터는 (채널, 1) 벡터로 줄여진다.
4. 추가적인 이슈
4.1. 이미지의 전처리
- CNN으로 CV 뉴럴넷을 훈련할 때는 주어지는 인풋 이미지의 전처리도 중요하다. 한 가지 전처리 방법은 정규화이다. RGB 컬러 이미지라면 픽셀값들은 0~255의 값을 가질텐데 0과 1 사이의 실수로 정규화해준 후에 컨볼루션을 시켜준다.
- 두번째 전처리 방법은 이미지 증강(Image Augmentation)이다. 1장에서 설명하기로, 컴퓨터가 정면으로 본 기차는 잘 인식하지만 옆면, 뒷면에서 본 기차는 잘 인식하기 못하는 문제가 있을 수 있다.
- 이 점을 방지하고 이미지를 어느 각도에서 보든 이미지를 잘 구분할 수 있는 본질적인 특성을 추출하기 위해 일부러 주어진 이미지들을 뒤집고, 반전시키고, 색깔을 바꾸고 하는 작업이 필요하다. 이 작업을 이미지 증강이라고 하는데, 증강을 거쳐서 다양한 패턴을 갖게 된 이미지를 학습하면 모델의 일반화 성능이 더 높아질 것으로 기대하는 것이다.
4.2. Deconvolution & FCN
- 디컨볼루션이란 컨볼루션의 반대 과정을 의미한다. 컨볼루션된 이미지를 원 차원으로 복구하거나, 아니면 그냥 주어진 이미지의 차원을 확대하는 방법이다.
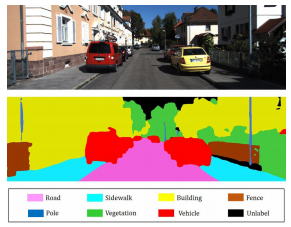
- Fully Convolution Network는 Convolution 계층과 Deconvolution 계층을 이어붙임으로써 Image Segmentation 문제에 자주 활용되는 뉴럴넷이다.
- 원 이미지를 컨볼루션하여 특성을 뽑아낸 후, 특성맵을 다시 원 차원으로 복구하면서 각 픽셀이 속한 범주에 대한 확률분포를 생성한다. 예측된 범주로 라벨링된 이미지를 반환하며, 실제 범주와의 비교를 통해 파라미터들을 훈련한다. 그 예시는 아래와 같다.
4.3. 전이학습(Transfer Learning)
- 가용한 데이터의 크기나 컴퓨터의 성능이 충분한 학습을 하기 어려울 때는 기존에 잘 만들어진 모델을 가져와 사용하는 방법을 쓸 수 있다. 이를 Pretrained Model이라고 하며, 주어진 구체적인 과제에 맞게 Pretrained Model에 추가적인 학습을 더하는 과정을 전이학습이라고 한다.
- 전이학습에는 크게 두 가지 방법이 있다. 첫째는 Freezing으로, pretrained model의 가중치들을 그대로 사용하는 것이다. pretrained model이 학습한 과제가 현재 해결하고자 하는 과제와 매우 유사한 경우에는 freezing이 합리적인 대안이 될 수 있다.
- 이때 pretrained model이 학습한 데이터는 현재 주어진 데이터와 유사하더라도, 라벨은 당연히 다르기 때문에 Convolution Layers는 freezing해서 사용하되 FC 레이어는 새로 만들어 이어붙인 후 FC 레이어만 훈련한다.
- 두번째는 Fine-Tuning으로, pretrained model의 컨볼루션 계층의 파라미터들도 주어진 데이터에 맞게 재훈련하되, 학습률을 훨씬 낮게 설정하여 미세하게 훈련을 진행하는 것을 말한다.
- 꼭 둘 중에 하나만 택해야 하는 것은 아니다. 컨볼루션 계층의 일부 파라미터들은 얼리고 나머지 일부 파라미터들은 fine-tuning을 하는 방식으로 혼합해서 쓰는 것도 당연히 가능하다.
4.4. 1D CNN
- CNN이 꼭 컴퓨터 비전 문제에만 사용되지는 않는다. 가령 시계열이나 NLP 문제에서 주어진 1차원 데이터들에 대해서도 적용될 수 있다. 그런데 이때 컨볼루션 과정에서, 데이터가 1차원이기 때문에 커널도 1차원의 한 방향으로만 움직이면서 특성을 추출한다는 점이 다르다.
- 1D CNN은 시계열이나 NLP 문제에 사용할 데이터들을 1차적으로 특성 추출 - 차원 축소하는 식으로도 많이 활용된다.
5. MNIST Fashion 데이터셋 분류하기
- 패션 아이템 이미지를 인식하여 분류하는 간단한 CNN 뉴럴넷을 구현해보자.
5.1. 라이브러리 임포트
#Pytorch 임포트
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
import torchvision.transforms as transforms
from torchvision import datasets
#GPU 사용
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device
5.2. 데이터 로드
- 이미지 데이터를 전처리하는 데에도 시간이 꽤 걸린다.
- 먼저 주어진 이미지를 torch가 이해할 수 있도록 tensor 타입으로 바꾸고, 정규화하는 것이 필요하다. 이를 transform이라고 한다.
from torch.utils.data import Dataset, DataLoader
import torchvision.transforms as transforms
from torchvision import datasets
#이미지를 tensor로 변환하며, 0~1로 자동 정규화
#흑백 채널의 평균과 표준편차를 각각 0.5로 두고 정규화 => 이미 0~1 범위를 가지므로 -1~1로 정규화
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5, ), (0.5, ))])
trainset = datasets.FashionMNIST(root='/content',
train = True, download = True, #train인지 test인지
transform = transform) #transform 적용
testset = datasets.FashionMNIST(root='/content',
train = False, download = True,
transform = transform)
#trainset에서 셔플한 후 사이즈가 64인 배치들을 가져와줌
train_loader = DataLoader(trainset, batch_size=64, shuffle=True)
test_loader = DataLoader(testset, batch_size=64, shuffle=True)
- transformed된 이미지 데이터를 셔플하고, 설정한 배치 사이즈에 맞게 가져오는 것도 필요하다. 이를 dataload라고 한다.
train_loader = DataLoader(trainset, batch_size=64, shuffle=True) #trainset에서 셔플한 후 사이즈가 64인 배치들을 가져와줌
test_loader = DataLoader(testset, batch_size=64, shuffle=True)
- 불러온 train set의 데이터들을 임의로 뽑아 확인하면 다음과 같다.
images, labels = next(iter(train_loader)) #train loader에서 이미지와 라벨을 쌍으로 하나씩 꺼내기
import matplotlib.pyplot as plt
labels_map = {
0: 'T-shirt',
1: 'Trouser',
2: 'Pullover',
3: 'Dress',
4: 'Coat',
5: 'Sandal',
6: 'Shirt',
7: 'Sneaker',
8: 'Bag',
9: 'Ankle Boot',
}
figure = plt.figure(figsize = (12, 12))
cols, rows = 4, 4
for i in range(1, cols * rows + 1):
image = images[i].squeeze() #이미지
label_idx = labels[i].item() #라벨
label = labels_map[label_idx] #라벨명 테이블에서 해당하는 라벨 가져오기
figure.add_subplot(rows, cols, i)
plt.title(label)
plt.axis('off')
plt.imshow(image, cmap = 'gray') #그림 그리기
plt.show()
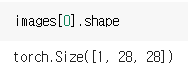
- 각각의 이미지는 채널 1, 가로 28, 세로 28의 사이즈를 갖는다. 채널이 1인 것은 흑백 이미지이기 때문이다(RGB라면 채널이 3이 됨).
5.3. 모델 구현
- CNN을 구현해보자.
5.3.1. 레이어 구축
- 모델 클래스의 초기화 연산자에서는 사용할 레이어들을 정의한다. 컨볼루션 뉴럴넷은 두 개의 레이어로, FC 레이어는 3개의 레이어로 구성해보자.
class NeuralNet(nn.Module):
def __init__(self):
super(NeuralNet, self).__init__()
self.conv1 = nn.Conv2d(1, 6, 3) #인풋 채널의 수, 아웃풋 채널의 수(커널 개수), 커널 사이즈
#스트라이드=1, 패딩=0, bias = true, 패딩모드 = 제로패딩
#아웃풋 차원 = (인풋 차원 - 커널 사이즈 + 2 * 패딩사이즈)/스트라이드 + 1
# = (28 - 3 + 2 * 0) / 1 + 1 = 26
self.conv2 = nn.Conv2d(6, 16, 3)
self.fc1 = nn.Linear(16 * 5 * 5, 120) #fc 레이어 시작:
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
- 먼저 컨볼루션 레이어:
- 주어진 이미지들은 채널이 1이므로 첫번째 컨볼루션 레이어의 채널도 1이어야 한다.
- 그 외에는 자유롭게 정해주면 되는데, 아웃풋 레이어의 채널의 길이(커널 개수), 커널 사이즈, 스트라이드, 패딩 등이다.
- 연속되는 두 레이어 간에는 아웃풋 채널 - 인풋 채널의 크기가 일치해야 한다. 그 외에는 신경쓸 것은 없다. 스트라이드를 지정해주지 않으면 디폴트값은 1이다.
- 그 다음에는 FC 레이어:
- FC 뉴럴넷의 인풋 레이어는 컨볼루션이 완료된 레이어와 차원이 같아야 한다. 위에서 컨볼루션된 레이어를 맥스풀링하고 나면 레이어의 차원이 (1, 400)이 된다.
- FC 뉴럴넷에서 연속하는 두 레이어 간에는 아웃풋 레이어 - 인풋 레이어의 차원이 맞아야 한다. 그 외에는 신경쓸 것은 없다.
- 맥스 풀링 레이어는 forward pass를 하면서 정의한다.
5.3.2. Forward pass
- 포워드 패스를 할 때는 각 레이어들을 거치면서 결과값의 차원이 의도한 대로 변화하고 있는지 계산해주는 것도 중요하다.
- 컨볼루션 레이어에서는 max pooling을 할 때와 fc 레이어로 넘겨줄 때 특히 신경을 써야하고,
- fc 레이어에서는 컨볼루션 레이어로부터 결과를 넘겨받을 때와 최종 아웃풋을 낼 때 특히 신경을 써줘야 한다.
- 컨볼루션을 마치고 FC 레이어로 넘겨줄 때, GAP를 사용할 수도 있지만 여기서는 그냥 flatten만 해주었다.
def forward(self, x):
x = self.conv1(x) #(28 - 3 + 2 * 0)/1 + 1 = 26*26
x = F.relu(x) #26 * 26
x = F.max_pool2d(x, 2) #2*2 사이즈의 맥스풀링 레이어로 스트라이드 (기본값=커널사이즈)2씩 이동, = 13 * 13 차원으로 축소
x = self.conv2(x) #(13 - 3 + 2 * 0)/1 + 1 = 11 * 11
x = F.relu(x) #11 * 11
x = F.max_pool2d(x, 2) #2*2 사이즈의 맥스풀링 레이어로 스트라이드 (기본값=커널사이즈)2씩 이동 = 5*5 차원으로 축소
x = x.view(-1, self.num_flat_features(x)) #flatten = 1 * 400
x = F.relu(self.fc1(x)) # 1 * 120
x = F.relu(self.fc2(x)) # 1* 84
x = self.fc3(x) # 1 * 10
return x
def num_flat_features(self, x):
size = x.size()[1:] #이미지 개수를 제외한, 채널과 가로와 세로 길이
num_features = 1
for s in size:
num_features *= s #를 다 곱해줌
return num_features
- 뉴럴넷을 완성하고 차원이 잘 맞아떨어지는지 확인하기 위해 초기값으로 결과를 내보았다.

- 최초에 인풋레이어가 (1, 1, 28, 28) = (이미지 개수, 채널, 가로, 세로)로 주어지면
- 컨볼루션 레이어를 거치면서 (1, 16, 5, 5)로 차원이 변화하고
- FC 레이어에서는 flatten되어 (1, 400)으로 변환된 후 최종적으로 (1, 10)의 벡터로 바뀐다.
- 이때 아웃풋이 (1, 10)이어야 하는 이유는 이미지를 10개 그룹 중 하나로 분류하는 것이기 때문이다. 각 원소의 값은 해당하는 그룹에 속할 확률을 의미한다.
5.4. 모델 학습
- SGD 옵티마이저를 사용하고, 학습률은 0.001, 모멘텀은 0.9, 에포크 수는 5로 한다. 성능치는 크로스엔트로피함수를 사용하는데, 이는 3개 이상의 그룹들도 분류를 하는 과제에서 자주 사용되는 성능치이다.
import torch.optim as optim
optimizer = optim.SGD(net.parameters(), lr = 0.001, momentum = 0.9)
criterion = nn.CrossEntropyLoss()
for epoch in range(5):
running_loss = 0.0
for i, data in enumerate(train_loader, 0):
inputs, labels = data
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
if i % 64 == 0:
print('Epoch: {}, iter: {}, Loss: {}'.format(epoch+1, i+1, running_loss/2000))
running_loss = 0.0- 배치 사이즈를 64로 했고 train set의 크기가 938이므로, 1 epoch마다 14번 정도의 iteration이 돌아간다.
5.5. 모델 검증
- 훈련된 모델을 검증한 결과는 아래와 같다. 아래 테이블은 test set의 이미지에 대해서 모델이 예측한 라벨값을 짝지은 것이다.
import matplotlib.pyplot as plt
labels_map = {
0: 'T-shirt',
1: 'Trouser',
2: 'Pullover',
3: 'Dress',
4: 'Coat',
5: 'Sandal',
6: 'Shirt',
7: 'Sneaker',
8: 'Bag',
9: 'Ankle Boot',
}
dataiter = iter(test_loader)
images, labels = next(dataiter)
outputs = net(images)
_, predicted = torch.max(outputs, 1)
figure = plt.figure(figsize = (12, 12))
cols, rows = 4, 4
for i in range(1, cols * rows + 1):
image = images[i].squeeze() #이미지
label_idx = predicted[i].item() #라벨
label = labels_map[label_idx] #라벨명 테이블에서 해당하는 라벨 가져오기
figure.add_subplot(rows, cols, i)
plt.title(label)
plt.axis('off')
plt.imshow(image, cmap = 'gray') #그림 그리기
plt.show()
- 대충 잘 맞는 것도 같다. 전체 테스트셋에서 모델이 맞춘 비율(accuracy)은 82% 정도가 나왔다.
'머신러닝&딥러닝' 카테고리의 다른 글
| Deep Learning #4 RNN(순환신경망) (0) | 2023.02.23 |
|---|---|
| Deep Learning #3 다양한 CNN: VGGNet, GoogleNet, ResNet (0) | 2023.02.22 |
| Deep Learning #1 딥러닝 기초: 심층신경망의 구조와 간단 코드 실습 (1) | 2023.02.15 |
| Machine Learning #5 클러스터링 : 근로자 임금 분포 클러스터링 (0) | 2023.02.12 |
| Machine Learning #4 차원 축소 : 신용카드 연체 여부 예측 (0) | 2023.02.09 |