1. Deep Neural Net
- 딥러닝(Deep Learning)이란 인공신경망(Artificial Neural Net)을 훈련해 회귀나 분류 문제 등을 해결하는 것을 말한다.
- 인공신경망은 심층신경망(Deep Neural Net) 또는 다층퍼셉트론(Multi-Layer Perceptron)이라고도 불린다. 굳이 구분할 필요는 없이 다 같은 개념으로 사용해도 된다고 본다.
- 심층신경망은 다음의 요소들로 구성된다.
- 인풋 레이어(Input Layer): 주어진 데이터가 벡터(Vector) 형태로 입력된다. 이를 인풋 벡터(Input Vector)라고도 말하며, 인풋 벡터 그 자체는 심층신경망의 입장에서는 인풋 레이어가 된다.
- 히든 레이어(Hidden Layer): 인풋 레이어와 아웃풋 사이를 매개하는 레이어. 인풋 레이어는 선형결합과 활성화함수를 거치며 복수의 히든 레이어들을 통과한다.
- 아웃풋 레이어(Output Layer): 히든 레이어들을 모두 거친 후 최종적으로 도달하게 되는 레이어. 이는 회귀나 분류 문제에서의 예측값으로 사용된다.
- 노드(Node): 주어진 레이어를 구성하는 원소들.
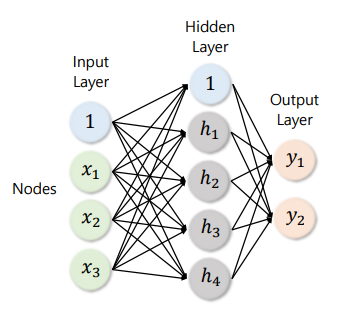
- 일반적으로는 그림보다 훨씬 많은 히든레이어들이 담겨있다(보통 히든레이어가 2개 이상일 때 Deep 뉴럴 넷이라고 말한다). 그럼 각각의 레이어들을 연결하는 저 화살표들이 무엇인지 알아보자.
1.1. 선형 결합(Linear Combination)
- 입력된 인풋 레이어는 선형 결합을 거쳐서 히든 레이어로 들어가고, 주어진 히든 레이어는 마찬가지로 선형결합을 거쳐 그 다음 레이어들로 차례차례 이동한다. 그럼 선형 결합이라는 게 뭔지 알아보자.
- 선형 결합이란 주어진 원소들의 가중치 합이라고 할 수 있다. 가령 벡터 $X$가 다음과 같이 주어져있을 때
$$X = [x_{1}, x_{2}, x_{3}, ..., x_{n}]$$
- 임의의 가중치 벡터 $W$에 대하여 $X$의 선형결합 $Z$는
$$Z = WX^{T} = w_{1}x_{1} + w_{2}x_{2} + ... + w_{n}x_{n}$$
이때, $W = [w_{1}, w_{2}, ..., w_{n}]$
- 주어진 레이어가 n차원 벡터일 때(즉 노드가 n개일 때), 선형결합을 통해 다음의 m차원 레이어로 도달했다고 하자. 이 n차원 벡터를 m차원 벡터로 보내기 위해서는 m*n 차원의 행렬을 곱해주면 된다. 즉 다음과 같은 연산이다.
$$\begin{bmatrix} w_{11} w_{12} ... w_{1n} \\ w_{21}w_{22} ...w_{2n} \\ ... \\ w_{m1}w_{m2} ...w_{mn} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\\vdots \\ x_{n} \end{bmatrix} =\begin{bmatrix} z_{1}\\ z_{2}\\\vdots \\ z_{m}\end{bmatrix}$$
이때 $z_{i} = w_{i1}x_{1} + w_{i2}x_{2} + ... w_{in}x_{n}$, for i = 1, 2, ... , m
- 주어진 레이어는 이런 행렬 연산을 통해 선형결합을 취하고 다음 레이어로 넘어가게 된다.
1.2. 활성화 함수(Activation Function)
- 일반적으로 주어진 레이어는 선형결합을 거치고나서 바로 다음 레이어로 넘어가지 않는다. 대개는 선형결합을 거치고 나서, 활성화 함수를 한 번 더 거쳐서 다음 레이어로 넘어가게 된다.
- 활성화 함수란, 선형결합으로 얻어진 각 노드의 값에 취하는 함수로 모델에 비선형성을 부여하기 위해 사용된다. 자주 사용되는 활성화 함수로는 Sigmoid, tanh, ReLU 등이 있다. 임의의 활성화 함수를 $f$라고 표현하면, 주어진 벡터 레이어 $X$를 다음 벡터 레이어 $Z$로 보내는 과정은 다음과 같다.
$$f(\begin{bmatrix} w_{11} w_{12} ... w_{1n} \\ w_{21}w_{22} ...w_{2n} \\ ... \\ w_{m1}w_{m2} ...w_{mn} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \\\vdots \\ x_{n} \end{bmatrix}) =\begin{bmatrix} f(z_{1})\\ f(z_{2})\\\vdots \\ f(z_{m})\end{bmatrix}$$
이때 $z_{i} = w_{i1}x_{1} + w_{i2}x_{2} + ... w_{in}x_{n}$, for i = 1, 2, ... , m
1.3. 예측과 오차
- 인풋 레이어가 선형결합과 활성화함수를 통해 히든 레이어들을 거치고 마지막 최종 레이어로 도달했다고 하자. 이때 최종레이어는 그 자체로 모델의 예측값이 된다.
- 최종레이어가 회귀문제의 예측값이 된다고 하자.
- 만약 어떤 스칼라값을 예측하는 것(가령, 주가)이 문제라면 최종 레이어의 차원이 1이 되도록 히든레이어들의 차원을 잘 조정해주면 된다.
- 만약 어떤 k차원 벡터값을 예측하는 것이 문제라면(가령, 주가와 금리와 환율을 한 방에 예측) 최종 레이어의 차원이 k가 되도록 히든레이어들의 차원을 잘 조정해주면 된다.
- 최종레이어가 분류문제의 예측값이 된다고 하자.
- 만약 주어진 샘플(인풋 벡터로 표현된)이 어떤 두 범주 사이에 어떤 범주에 속할지 예측하는 것(가령, 주가가 오를지 내릴지)이 문제라면 최종 레이어의 차원이 2가 되면서 두 노드가 확률을 나타내도록 하면 된다(두 노드 각각은 0과 1 사이의 실수이면서 두 노드의 합은 1이 되도록).
- 만약 주어진 샘플이 어떤 k개의 범주 사이에 어떤 범주에 속할지 예측하는 것(가령, 주가가 오를지 내릴지)이 문제라면 최종 레이어의 차원이 k가 되면서 k개의 노드가 확률을 나타내도록 하면 된다(k 노드 각각은 0과 1 사이의 실수이면서 k개 노드의 합은 1이 되도록).
- 앞에서 말한 활성화함수들은 이 지점에서도 유용하게 쓰인다. 왜냐하면 히든 레이어들을 거쳐온 최종 레이어의 노드들이 0과 1 사이의 값을 가진다는 보장이 없기 때문에 로지스틱 함수나 소프트맥스 함수 등을 적용하게 된다. 언급한 함수들은 정의역이 모든 실수이고 치역이 0과 1 사이의 수인 함수들이기 때문이다.
- 하지만 초기에 한 번 이런 레이어들을 거쳤다고 해서 최종레이어가 좋은 예측값이 되지는 않는다. 그래서 실제 값과 예측값의 차이인 오차가 발생하게 된다. 이 오차를 줄이기 위해서 모델의 파라미터들을 수정하게 된다. 이때 파라미터란 선형결합에 사용되는 가중치행렬의 원소들을 말한다. 그리고 모델이 오차를 최소화할 때까지 이 파라미터들을 지속적으로 아주아주 오랜 시간 수정한다. 그러다보면 언젠가는 오차가 꽤 작은 값까지 줄어들게 된다.
- 그 과정은 다음 장에서 공부해보자.
2. 경사하강법과 오차역전파(Back Propagation)
- 뉴럴넷의 예측 오차를 최소화하도록 하는 것이 곧 뉴럴넷을 훈련하는 것이다. 그런데 일반적으로는 예측 오차를 최소화한다기보다는 어떤 계산된 비용함수(Cost function)를 사용한다.
- 회귀문제의 경우에서 자주 사용되는 비용함수는 평균오차제곱(MSE; Mean Squared Error)이다. i번째 샘플에 대해서 모델의 예측값이 $\hat{y_{i}}$이고 실제값이 $y_{i}$일 때 MSE는 다음과 같이 정의한다.
$$MSE = \Sigma_{i=1}^{N} (y_{i}-\hat{y_{i}})^{2}$$
- 꼭 이런 비용함수를 사용할 필요는 없다. 문제에 따라 비용함수는 다를 수 있다. 하여간 뉴럴넷은 경사하강법이라는 과정을 거쳐서 이 비용함수를 최소화한다.
2.1. 경사하강법(Gradient Descent Method)
- 경사하강법이란 주어진 비용함수의 그래디언트를 계산하고, 그래디언트가 가리키는 반대 방향으로 파라미터들을 조정하는 것을 말한다.
- 그래디언트란 다변수함수 $f(x_{1}, x_{2}, ... , x_{n})$를 각각의 독립변수들에 대해 편미분한 값을 원소로 하는 벡터를 말한다. 즉
$$\frac{\partial f(X)}{\partial X} = \begin{bmatrix} \frac{\partial f}{\partial x_{1}} \\ \frac{\partial f}{\partial x_{2}} \\ \vdots \\ \frac{\partial f}{\partial x_{n}} \end{bmatrix} $$
- 이 그래디언트는 벡터인데, 각각의 독립변수들을 아주 작은 단위로 증가시켰을 때 정의된 함수 $f$가 증가하는 방향을 말한다.
- 비용함수를 가중치 행렬에 대하여 편미분해서 그래디언트를 구한 후, 이 그래디언트가 가리키는 반대 방향으로 가중치들을 변화시키면 비용함수를 감소시킬 수 있게 된다는 뜻이다. 다시 말해 새로운 가중치 행렬은 다음과 같다.
$$W_{next} = W_{current} - \gamma \frac{\partial E(W)}{\partial W}$$
이때, E(W)는 비용함수를 나타내며 가중치 행렬의 함수이다.
- $\gamma$는 학습률(learning rate)인데, 그래디언트 방향으로 얼마나 빠르게 가중치를 조정할지를 결정하는 하이퍼 파라미터이다.
- 뉴럴넷은 그래디언트를 계산해서 가중치 행렬을 수정한다. 그 다음에 다시 수정된 가중치 행렬 하에서 그래디언트를 계산해서 한 번 더 가중치 행렬을 수정한다. 이 과정을 주어진 epoch(훈련 한 타임)수만큼 반복하며, 정의한 비용함수가 더이상 작아지지 않을 때까지 지속한다.

- 위 그림은 1개의 가중치를 가지고 있는 비용함수를 표현한 것이다. 주어진 가중치에서 비용함수를 편미분해 얻은 기울기가 그래디언트이고, 그래디언트에 학습률을 곱한 만큼 가중치를 변화시키면서 비용함수의 극소점을 향해 다가간다.
2.2. 오차역전파(Back Propagation)
- 그런데 그래디언트를 계산하는 것이 보통 어려운 일이 아니다. 왜냐면 각각의 가중치들은 비용함수에 직접 매개하는 것이 아니기 때문이다. 업데이트하려는 가중치와 비용함수 사이에는 수많은 히든레이어들이 존재하고, 가중치를 변화시켰을 때 이 히든레이어들을 거쳐서 비용함수에 최종적으로 미치는 영향력을 계산하는 것이 꽤 복잡하다.
- 그래서 사용하는 것이 연쇄법칙(Chain Rule)이다. 독립변수 $X$와 종속변수 $Y$ 사이에 매개변수 $Z$가 존재할 때, $Y$의 $X$에 대한 편미분은 $Z$의 $X$에 대한 편미분과 $Y$의 $Z$에 대한 편미분의 곱이다. 즉
$$\frac{\partial Y}{\partial X} = \frac{\partial Y}{\partial Z} * \frac{\partial Z}{\partial X}$$
- 뉴럴넷에서 그래디언트는 다음과 같이 계산한다.
- 먼저 주어진 레이어의 가중치들로 다음 레이어의 노드 값을 편미분해서 저장해둔다. 이런 편미분은 인풋레이어의 가중치부터 비용함수에 도달할 때까지 계속된다. 이 과정을 Forward Pass라고 한다.
- Forward Pass를 거친 후, 어떤 주어진 가중치에 대한 비용함수의 편미분계수는 그 가중치로부터 비용함수까지 연결되어 있는 모든 편미분계수의 곱이 된다. 이 과정을 Backwardpass 또는 오차역전파(Back Propagation)이라고 한다.
- 각각의 가중치에 대응하는 편미분계수들을 모두 계산한 후에 벡터로 정리하면 그래디언트가 완성된다.
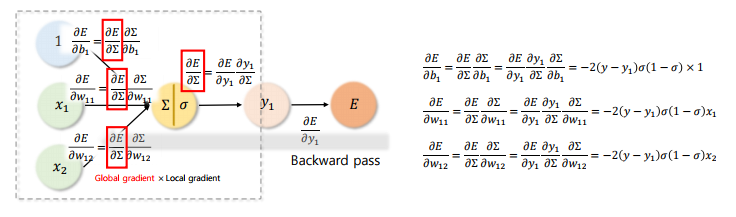
- 어떤 가중치의 입장에서, 다음 레이어를 가중치에 대해 편미분한 것을 Local Gradient, 그리고 그 다음 레이어에 대해서 비용함수를 편미분한 것(즉 그 레이어로부터 비용함수까지 도달하는 모든 편미분계수의 곱)을 Global Gradient라고도 부른다. 위 그림에서 $\sigma$ 어쩌구가 붙은 것은 가정한 활성화함수의 편미분이 이것이기 때문이다.
3. 추가적인 고려사항들
- 2장의 내용은 뉴럴넷의 아주 본질적인 내용들을 다룬 것이다. 뉴럴넷의 골격을 이해했으므로 뉴럴넷의 훈련을 효율화하기 위한 추가적인 이슈들을 소개한다.
3.1. Gradient
- 뉴럴넷을 훈련하면서 겪는 문제 중의 하나는 그래디언트 소실 또는 그래디언트 폭주이다. 그래디언트는 편미분계수들의 곱으로 정의되는데, 비용함수로부터 멀리 떨어진 레이어의 가중치들은 너무 많은 편미분계수들을 곱하다보면 그래디언트가 너무 작아지거나(소실) 너무 커지는(폭주) 문제가 발생한다.
3.1.1. ReLU
- 한 가지 방법은 활성화함수를 ReLU 함수로 사용하는 것이다. ReLU 함수는 다음과 같이 생겼는데, 보면 알겠지만 0보다 작은 값은 0으로, 0보다 큰 값은 그대로 반환하는 함수이다. ReLU 함수의 기울기는 0 또는 1이므로, 글로벌 그래디언트에 곱해지는 값은 항상 0 또는 1이 되기 때문에 그런 문제가 적다.
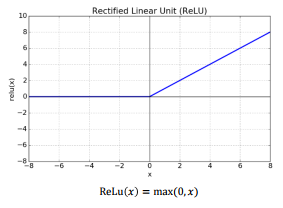
- 물론 ReLU 함수도 문제가 있다. 가중치의 값이 0보다 작아지게 되면 그래디언트가 0이 되어버린다. 이런 문제를 Dying ReLU 문제라고 한다. 이를 해결하기 위해서 0보다 작은 값에서도 미세하게나마 기울기를 갖는 leaky ReLU 함수 등을 사용하기도 한다.
3.2.3. Gradient Clipping
- 클리핑은 그래디언트 폭주 문제를 방지하기 위한 것인데, 그래디언트가 일정 임계값을 넘지 못하도록 잘라내는 것이다.
3.2. 훈련 비용
- 뉴럴넷의 히든레이어가 많을수록, 인풋벡터의 차원이 클수록, epoch 수가 많을수록 훈련 과정이 매우 길어진다.
3.2.1. 미니배치(Mini Batch)
- 우선 배치란 한 번 학습을 하는 데 사용되는 샘플들의 수를 말한다. 한 번 학습을 할 때 모든 샘플들을 사용하면 Full-Batch, 샘플들을 나누어서 사용하면 Mini-Batch라고 한다. 풀 배치를 사용하면 한 번 훈련할 때 모든 샘플들을 다 사용하므로 시간이 너무 오래 걸린다. 따라서 샘플들을 나누어서 미니 배치만을 사용해 한 번 훈련을 하는 것이 일반적이다.
- epoch는 한 번 훈련을 마친 것이라고 했는데, 이것은 풀배치일 때의 이야기이고 미니배치를 사용할 때는 epoch당 n번의 미니배치를 훈련하게 된다.
- epoch을 한 번 완수하기 위해서 미니배치가 몇 개 필요한가를 나타내는 것이 iteration이다.
- iteration = 5, epoch = 100, mini-batch size = 200이면, 100번의 epoch을 돌리는데 epoch마다 200개의 샘플을 5번 집어넣어 훈련(가중치 업데이트)시킨다는 뜻이다.
- 미니배치를 사용하는 경사하강법을 확률적 경사하강법(SGD)라고도 부른다. 이는 전체 샘플 중에 어떤 샘플들을 미니배치로 사용할지를 결정하는 것이 랜덤하기 때문이다.
3.2.2. 학습률 Scheduling
- 학습률 스케쥴링이란, 에포크마다 학습률을 조정하는 것을 말한다. 보통 초반에는 학습률을 크게 해서 비용함수의 최저점을 향해 성큼성큼 다가가다가 나중에는 학습률을 줄여서 미세하게 저점을 찾는 것을 의미한다.
- 스케쥴링에 Warmup 기법이 사용되기도 한다. 이는 학습 초반에 빠르게 학습률을 끌어올리고, 이후에 천천히 학습률을 감소시키는 방식이다.
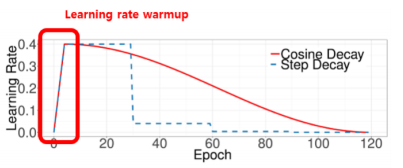
- 학습률 스케쥴링의 특수한 예로 Cosine Annealing decay라는 것이 있다. 학습률을 증가시켰다 감소시켰다를 반복하는 스케쥴링 기법인데, local minima 문제에 효과가 있다고 알려져있다.
3.2.3. Momentum
- 모멘텀이란 지역 최소값에 갇히게 되는 문제를 방지하는 것이다. 비용함수가 Convex한 형태를 가질 때 그래디언트를 따라 가중치를 업데이트하다보면 언젠가는 전역 최소값(Global Minima; 비용함수의 최소값)에 도달하게 될 것이다. 그러나 비용함수가 아래와 같이 생겼다면, 그래디언트만 따라가서는 전역 최소값까지 가지 못하고 중간에 움푹 패인 지점에 갇히게 된다. 이 지점을 지역 최소값(Local Minima)라고 한다.
- 이를 방지하기 위해서, 모멘텀의 개념을 사용한다. 이는 직전에 계산된 그래디언트가 컸다면 그 다음에는 더 크게 가중치를 조정하도록 하는 것이다.
3.2.4. Optimizer
- 앞서 언급한 SGD나 Momentum 등을 사용해서 경사하강법을 진행하도록 최적화 방법을 셋팅해둔 것들을 Optimizer라고 한다. 자주 사용되는 것은 Adam Optimizer이다.
3.2.5. 조기 종료
- 사전에 정해둔 성능에 도달하게 되면 훈련을 조기 종료하도록 설정하기도 한다.
3.3. 과대적합
3.3.1. 규제항
- 비용함수에 규제항(가중치들의 크기를 반영하는 함수)을 추가하여, 가중치들이 너무 커지지 않도록, 특히 특정한 소수의 몇몇 노드로 가중치가 편중되지 않도록 하는 것이다.
- 소수 노드에 붙는 가중치가 너무 커진다는 것은, 그 노드 값에 예측이 너무 의존하게 된다는 것이다. 따라서 샘플의 특성이 조금만 달라져도 성능이 크게 약화될 수 있다.
3.3.2. Drop-out
- 드롭아웃 기법은 훈련을 할 때마다 임의로 몇 개의 노드들을 끄는 것(0으로 만드는 것)을 말한다. 이런 방법을 사용하면 특정한 노드에 붙는 가중치가 너무 커지고 다른 노드들을 무시하게 되는 문제를 방지할 수 있다.
3.4. Batch Normalization
- 우선 배치 정규화란, 레이어가 선형결합을 거친 후 활성화함수에 들어가기 직전에 정규화(평균을 빼고, 표준편차로 나누고)를 실시하는 작업을 말한다.
- 가령 100개의 샘플들로 미니배치를 구성해서 훈련 중이라면, 선형결합을 거친 100개의 값들이 자신들의 표본 평균과 표준편차를 계산해 정규화를 거치고, 그 후에 활성화함수로 입력된다.
- 이런 작업이 어떤 의미가 있을까? 배치 정규화는 첫째로 그래디언트 소실 문제에 대응한다. 각각의 샘플들이 레이어들을 통과하다보면 그 결과로 나온 값들(Activation Value)의 분포가 한쪽으로 치우치거나 너무 퍼지는 등의 문제가 발생한다. 그러면 그 상태에서 계산된 그래디언트가 너무 작아지는 문제도 발생하게 될 것이다. 가령 활성화함수의 하나인 시그모이드 함수는 극단적인 값으로 갈수록 미분값이 0으로 수렴한다. 따라서 활성화함수에 들어가기 이전에 분포가 엉망이 된 배치들을 모아 정규화해주고 활성화함수에 넣어주면 그래디언트 소실 문제를 완화할 수 있다.
- 둘째로 배치정규화를 사용하면 학습률을 높여서 빠른 학습을 진행할 수 있다. 배치 정규화를 하지 않을 경우에는 배치를 구성하는 샘플들마다 발생시키는 그래디언트가 다 다르다. 우리는 샘플 전체의 오차제곱의 평균을 줄여야 하는 것이므로, 이런 상황에서는 학습률을 함부로 높일 수가 없고 조심스럽게 학습을 진행시켜야 한다.
- 그런데 배치 정규화를 해줌으로써 흩어져있던 샘플들을 모아 그래디언트가 유사하도록 만들어주면 학습률을 높여서 빠르게 학습을 진행할 수 있다.
- 이런 다양한 장점들로 인해 배치 정규화는 대부분의 뉴럴넷 구현에서 사용된다.
3.5. Weight Initialization
- 배치 정규화와 유사한 의도로 사용되는 기법이 가중치 초기화이다. 가중치를 단순히 임의로 초기화하는 것이 아니고 어떤 분포를 따르는 가중치들로 초기화하는 것이다. 적당하게 초기화된 가중치들은 레이어들을 거친 후에도 Activation Value들이 마치 정규화된 값들처럼 분포하도록 돕는다고 알려져있다.
- 자주 사용되는 초기화 방법은 Xavier 초기화와 He 초기화가 있다. Xavier 초기화는 tanh 함수, He 초기화는 ReLU 함수와 함께 사용될 때 효과가 좋다고 한다.
4. 간단한 실습
- 간단한 선형회귀모형을 뉴럴넷으로 구현해보자.
- 뉴럴넷을 구현하기 위해서는 파이썬의 딥러닝 프레임워크인 파이토치(Pytorch)에도 익숙해져야 한다. 객체 지향 프로그래밍에 익숙하지 않으면 파이토치를 사용하는 것도 조금 버벅거리게 되기 때문에 나같은 문돌이는 이론뿐만 아니라 코드 구현도 마냥 쉽지는 않다.
4.1. 데이터 준비
- torch를 비롯한 라이브러리들을 불러온다.
import torch #Pytorch
import matplotlib.pyplot as plt
import numpy as np- 실습에 사용할 데이터를 만들어보자. X값으로 Y값을 맞추는 선형회귀 문제이므로 다음과 같이 생성한다.
- pytorch 내에서 사용할 데이터들은 텐서(Tensor)로 표현된다. 텐서란 차원을 가지면서 정보를 담는 어떤 공간적인 개념이라고 생각하면 된다. 텐서가 1차원이면 벡터인 것이고, 2차원이면 행렬인 것이고, 3차원이면,... 등등이다.
- 텐서를 생성하기 위해서는 torch.method()를 사용한다. 여기서는 randn 메소드를 사용해서 표준정규분포를 따르는 랜덤한 확률변수들을 생성해 1차원 텐서에 담았다.
- 텐서를 다시 numpy array로 불러오기 위해서는 numpy() 메소드를 사용한다.
X = torch.randn(200, 1) * 10
y = X + 3 * torch.randn(200, 1)
plt.scatter(X.numpy(), y.numpy())
plt.ylabel('y')
plt.xlabel('x')
plt.grid()
plt.show()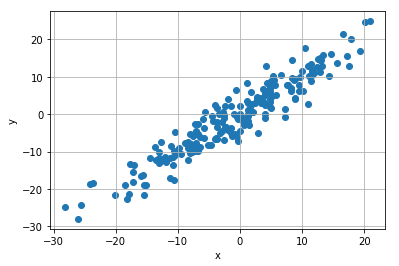
4.2. 뉴럴넷 구현하기
- 뉴럴넷을 구현할 때는 우선 nn.Module을 상속하는 클래스를 정의한다. nn.Module은 우리가 뉴럴넷을 구현하기 위해 필요한 다양한 메소드들을 이미 가지고 있는 클래스이므로 이를 상속함으로써 우리의 작업을 편리하게 할 수 있다.
- 초기화함수에서는 뉴럴넷의 각 레이어들을 정의해준다. 선형회귀문제이믈 선형결합을 수행하는 5개의 레이어들을 만들었다.
- 이때 먼저 구상해야할 것이 우리에게 주어진 인풋의 차원과 아웃풋의 차원이다. 문제에서 인풋은 각 샘플 $X$이므로 1차원이다. 그리고 아웃풋은 각 샘플 $Y$이므로 마찬가지로 1차원이다. 그러면 인풋레이어의 차원은 1, 아웃풋 레이어의 차원은 1이어야 하고 그 사이의 히든레이어들은 인풋레이어와 아웃풋레이어의 차원이 어그러지지 않도록 잘 맞춰줘야 한다.
import torch.nn as nn
class LinearRegressionModel(nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
self.linear1 = nn.Linear(1, 4)
self.linear2 = nn.Linear(4, 8)
self.linear3 = nn.Linear(8, 4)
self.linear4 = nn.Linear(4, 2)
self.linear5 = nn.Linear(2, 1)
def forward(self, x):
x = self.linear1(x)
x = self.linear2(x)
x = self.linear3(x)
x = self.linear4(x)
x = self.linear5(x)
return x
linear_net = LinearRegressionModel()
print(linear_net)
print(list(linear_net.parameters()))- init 연산자에서 정의된 레이어들을 보면, 먼저 인풋 레이어는 1차원 벡터를 받아서 4차원의 벡터로 반환하는 레이어이다. 2번째 레이어는 4차원 벡터를 받아서 8차원 벡터로 반환하는 레이어이다. 이런 식으로 넘기다가 마지막 5번째 레이어, 즉 아웃풋 레이어는 2차원 벡터를 받아서 1차원 벡터로 반환하는 레이어이다.
- forward 함수는 forward pass를 진행하는 함수이다. 인풋레이어부터 아웃풋레이어까지 주어진 인풋 벡터 x를 차례차례 통과시킨다.
- 모델의 정보는 아래와 같이 출력할 수 있다.

- 각 레이어가 담은 가중치들로 출력할 수 있다. 예컨대 1번째 레이어는 1차원 벡터를 4차원 벡터로 보내기 위한 4*1 가중치 행렬과, bias 4개를 담고 있다. bias는 그냥 상수항으로, 계산된 선형결합 항에 추가로 더해주는 값이다.

- 뉴럴넷을 생성하면 초기 가중치는 아무렇게나 만들어진다. 이 뉴럴넷이 내놓는 예측값을 실제값과 비교해보자.
y_pred = linear_net(X)
plt.plot(X, y_pred.detach().numpy(), label = 'fitted')
plt.plot(X, y, '.', label = 'data')
plt.legend()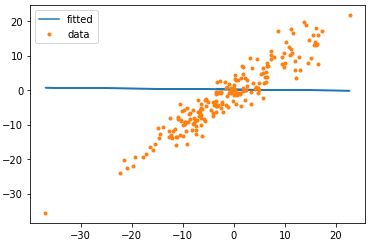
- 엉망진창으로 예측을 하고 있다. 파란선(사실 파란점인데 이어놓은 것임)이 예측값이고 오렌지 점들이 실제값이다,
4.3. 뉴럴넷 훈련하기
- 이 못난이 초기 뉴럴넷을 훈련하자. 첫번째는 손실함수와 최적화함수로 무엇을 쓸 것인지 정해야 한다. 손실함수는 MSE로, 최적화함수는 SGD를 사용한다. 학습률은 0.001로 했다.
import torch.optim as optim
criterion = nn.MSELoss()
optimizer = optim.SGD(linear_net.parameters(), lr = 0.001)- 본격적으로 모델을 훈련한다. epoch은 100개로 하고, 매 에포크마다 손실을 저장하여 출력해보자. 이때 풀 배치 경사하강법을 사용하므로, iter는 의미가 없다.
- 아래 코드를 설명하면,
- zero_grad(): 그래디언트를 초기화한다. 매 에포크마다 파라미터들을 업데이트한 후에 직전 에포크에서 계산한 그래디언트를 없애고 새로운 그래디언트를 만들겠다는 뜻이다.
- 그 다음에 예측값을 생성하고(forward pass), 미리 정의한 손실함수를 통해 손실값을 계산하고, 저장한다.
- back.ward(): 앞에서 예측값을 생성하면서 자동으로 편미분계수들이 저장된다. 여기서는 그 편미분계수들을 누적곱하여 그래디언트를 계산한다(backprop).
- step(): 계산된 그래디언트에 따라 가중치행렬을 업데이트한다.
epochs = 100
losses = []
for i, epoch in enumerate(range(epochs)):
optimizer.zero_grad()
y_pred = linear_net(X)
loss = criterion(y_pred, y)
losses.append(loss.item())
loss.backward()
optimizer.step()
print('Epoch: {}, Loss: {}'.format(epoch+1, loss.item()))- 100번의 에포크동안 손실값들이 줄어드는 과정을 보여준다.
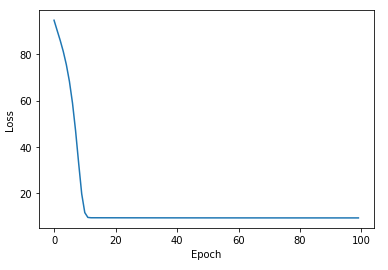
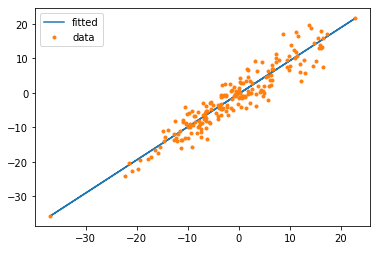
- 100번 동안 가중치행렬을 고친 후, 얻어진 최종 뉴럴넷으로 예측한 값을 다시 그려본다. 이제는 꽤 잘 맞는다.
'머신러닝&딥러닝' 카테고리의 다른 글
| Deep Learning #3 다양한 CNN: VGGNet, GoogleNet, ResNet (0) | 2023.02.22 |
|---|---|
| Deep Learning #2 CNN(합성곱 신경망) (0) | 2023.02.17 |
| Machine Learning #5 클러스터링 : 근로자 임금 분포 클러스터링 (0) | 2023.02.12 |
| Machine Learning #4 차원 축소 : 신용카드 연체 여부 예측 (0) | 2023.02.09 |
| Machine Learning #3 Decision Tree & Ensemble : 신용카드 연체 예측 (0) | 2023.02.08 |