GitHub - SeungbeomDo/DataAnalysis: Practical Codes for Data Analysis using Machine Learning and Deep Learning
Practical Codes for Data Analysis using Machine Learning and Deep Learning - GitHub - SeungbeomDo/DataAnalysis: Practical Codes for Data Analysis using Machine Learning and Deep Learning
github.com
1. RNN의 개요
1.1. Sequence Data
- 시퀀스 데이터란 데이터가 배열된 순서에도 정보가 담겨 있는 데이터를 말한다.
- 가령 번역기는 영어 문장을 인풋 데이터로 받아서 한국 문장을 아웃풋으로 내놓는 모델인데, 문장에 담겨 있는 단어의 순서가 그 자체로 중요한 정보가 된다. 왜냐하면(영어 문장의 경우) 어떤 단어가 주어라면 그 다음에 오는 단어는 동사로 해석해야 할 확률이 높고, 그 다음에 오는 단어는 보어나 목적어 등등으로 해석해야 할 확률이 높기 때문이다.
- 반면 이미지 데이터는 순서가 그렇게 중요하지 않다. 강아지 이미지를 고양이 이미지보다 먼저 인식하는 것이 특별한 의미를 갖지 못하기 때문이다.
- 시퀀스 데이터를 처리하는 데 특화된 뉴럴넷의 종류가 바로 RNN(Recurrenct Neural Net; 순환신경망)이다. RNN은 인풋 벡터가 주어지는 순서 자체가 학습에 활용될 수 있도록 하는 특수한 형태를 가지고 있다.
1.2. RNN의 구조
- RNN은 다음과 같은 구조를 가지고 있다.

- 인풋 벡터가 $[X_{0}, X_{1}, ... , X_{n}]$로 주어져있다고 하자. 그러면 인풋 벡터의 각 원소들은 순서대로 뉴럴넷에 들어온다.
- $X_{0}$이 들어오면 뉴런을 거쳐 $X_{0}$에 해당하는 아웃풋 $y_{0}$을 반환한다. 그와 동시에 어떤 임시적인 아웃풋인 $h_{0}$을 저장한다. 이를 hidden state라고 한다.
- hidden state는 현재까지 주어진 인풋의 함수인데 현재의 아웃풋 $y_{0}$와 동일할 수도 있고, 또 어떤 다른 값일 수도 있다.
- $X_{1}$이 들어오면 뉴런을 거쳐 아웃풋 $y_{1}$을 반환한다. 근데 이때 이전 기에서 발생한 hidden state가 $y_{1}$을 산출하는 데 영향을 준다. 또한 다음기로 보내기 위한 hidden state $h_{1}$도 생성된다.
- 이때 hidden state는 0번째 인풋과 1번째 인풋 둘 다의 함수가 되었다. hidden state는 단지 현재 주어진 인풋의 함수가 아니라 지금까지 주어진 모든 인풋의 함수이다.
- 따라서 RNN은 크게 보아 두 개의 가중치를 가진다. 하나는 현재 주어진 인풋 벡터 $X_{t}$에 사용될 가중치 행렬 $W_{x}$이고, 다른 하나는 이전 기의 hidden state $h_{t-1}$에 사용될 가중치 행렬 $W_{h}$이다.
- 이상을 수식으로 표현하면 아래와 같다. t기의 아웃풋은 t기의 인풋과 t-1기까지 주어진 hidden state의 함수이다. t-1기의 hidden state는 t-1기까지 주어진 모든 인풋들의 함수이므로, 사실 t기의 아웃풋은 t기까지 주어진 모든 인풋들의 함수인 셈이다.
$$Y_{t} = f(W_{x}X_{t} + W_{h}h_{t-1} + b)$$
- 한 가지 주의할 것은 가중치 행렬 $W_{x}$와 $W_{h}$는 t에 대하여 변화하지 않는 상수라는 것이다. 즉 매 기의 인풋마다 다른 가중치 행렬이 적용되는 것이 아니다. 이런 점을 반영하여 RNN을 다음과 같이 나타내기도 한다.

1.3. RNN의 유형
- RNN은 인풋과 아웃풋이 어떤 형태를 갖느냐에 따라서 4가지 형태로 분류된다.
- 첫째는 인풋도 시퀀스이고 아웃풋도 시퀀스인 시퀀스-시퀀스(Sequence to Sequence) 모델이다. Many-to-Many라고도 부른다.
- 가령 주가시계열을 예측한다면, 1일부터 N일까지의 주가가 인풋이고, 2일부터 N+1일까지의 주가가 아웃풋이 된다.

- 둘째는 인풋은 시퀀스이고 아웃풋은 벡터인 시퀀스-벡터 모델이다. Many-to-One 모델이라고도 부른다.
- 가령 어떤 음식점의 리뷰로 주어진 문장(단어의 시퀀스)을 받아들인 후, 그래서 이 고객이 만족을 했다는 건지 어쨌다는 건지 하나의 결과를 반환해주는 경우이다.

- 셋째는 인풋은 벡터이고 아웃풋은 시퀀스인 벡터-시퀀스 모델이다. One-to-Many 모델이라고도 부른다.
- 가령 연준에서 금리 인상분을 결정했을 때(벡터), 1일 후, 2일 후, ... , n일 후의 주가를 예측하는 경우이다. 상당히 해결하기 난감한 과제인데 일단 예시가 이것밖에 안 떠올라서.

- 넷째는 인풋과 아웃풋이 모두 벡터인.. 경우가 아니다. 하나를 받아서 하나로 내놓는 경우라면 굳이 RNN을 쓸 이유가 없다. 진짜 네번째 모델은 인코더-디코더(Encoder-Decoder)라고 부르는 특수한 형태이다.
- 인코더-디코더 모델은 인풋을 받아서 인코딩하여 저장하는 인코더 파트와, 인코딩된 시퀀스들을 시퀀스 아웃풋으로 내놓는 디코더 파트로 구성된다. 이런 형태는 특히 번역을 할 때 장점을 갖는다. 단어를 곧바로 번역하기보다는 단어를 몇 개 받아놓고, 맥락까지 고려하여 한 번에 번역하는 것이 더 타당한 결과를 줄 수 있기 때문이다.

2. RNN의 훈련 방법
2.1. BPTT
- 일반적인 뉴럴넷은 주어진 인풋 벡터가 복수의 레이어를 차례대로 통과하면서 하나의 예측값을 반환하고, 발생한 오차를 가지고 레이어들을 역순으로 훈련한다(Backpropagation). 하지만 RNN은 주어진 레이어들을 여러개의 인풋 벡터가 차례대로 통과하면서 예측값을 반환하기 때문에 일반적인 뉴럴넷과는 훈련 방법이 다르다.
- 주어진 인풋 벡터들이 순서대로 레이어를 통과하기 때문에, RNN의 훈련 방법을 시간에 따른 오차 역전파(BPTT; Back Propagation Through Time)
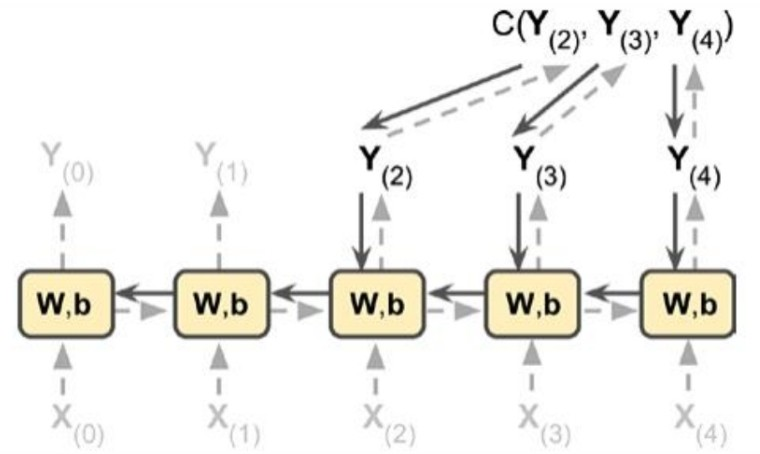
- 위 그림은 BPTT의 한 예시이다. RNN은 인풋과 아웃풋이 시퀀스를 갖는지 여부에 따라 다양한 형태를 가지기 때문에 오차역전파가 이루어지는 과정도 다 다를 수 있다. 위의 예시는 인풋 벡터가 시퀀스이고 아웃풋은 잠재적인 아웃풋 시퀀스의 일부로만 구성된 경우이다.
- 한편, 위 그림에서는 인풋에 곱해지는 가중치행렬과 hidden state에 곱해지는 가중치행렬을 구분하지 않고 $W$로 합쳐서 나타낸 것임에 유의하자.
- Forward Pass가 진행되면서 각 가중치 레이어의 편미분이 계산되고(실선을 따라), 예측 오차를 발생시킨 후에는 예측 오차 발생에 개입한 모든 가중치 레이어들을 따라 Back Propagation이 진행된다(점선을 따라).
- 예측 오차는 $Y_{2}$, $Y_{3}$, $Y_{4}$에 대해서만 발생하므로 $Y_{0}$, $Y_{1}$은 고려되지 않는다.
2.2. BPTT에서 그래디언트 계산
- 위의 상황에서 그래디언트를 수식으로 표현하자면 다음과 같을 것이다. 우선 비용함수는 3개의 아웃풋에 대한 비용함수들의 합니다. 즉
$$E = E_{2} + E_{3} + E_{4}$$
- 가중치 행렬에 대하여 편미분한 것은 다음과 같다.
$$\frac{\partial E}{\partial W} = \frac{\partial E_{2}}{\partial W} + \frac{\partial E_{3}}{\partial W} + \frac{\partial E_{4}}{\partial W}$$
- 총 3개의 편미분계수가 존재한다. $E_{2}$의 편미분계수만 적어보면
$$\frac{\partial E_{2}}{\partial W} = \frac{\partial E_{2}}{\partial Y_{2}} \frac{\partial Y_{2}}{\partial W} + \frac{\partial E_{2}}{\partial Y_{2}}\frac{\partial Y_{2}}{\partial Y_{1}} \frac{\partial Y_{1}}{\partial W} + \frac{\partial E_{2}}{\partial Y_{2}}\frac{\partial Y_{2}}{\partial Y_{1}}\frac{\partial Y_{1}}{\partial Y_{0}} \frac{\partial Y_{0}}{\partial W}$$
- $E_{2}$는 $Y_{2}$의 함수인데 $Y_{2}$는 $Y_{1}$과 $Y_{0}$의 함수이기도 하다. 따라서 $E_{2}$는 이 세 가지 변수들의 함수이다. 주어진 가중치행렬은 이 변수들을 모두 거쳐서 $E_{2}$에 영향을 준다. 따라서 가중치행렬에 대한 편미분은 각각의 변수들을 거치는 모든 경로들에 대하여 합산된다.
3. LSTM과 GRU
3.1. LSTM
3.1.1. 그래디언트 문제
- 앞에서 본 그래디언트 계산식을 가져오면
$$\frac{\partial E_{2}}{\partial W} = \frac{\partial E_{2}}{\partial Y_{2}} \frac{\partial Y_{2}}{\partial W} + \frac{\partial E_{2}}{\partial Y_{2}}\frac{\partial Y_{2}}{\partial Y_{1}} \frac{\partial Y_{1}}{\partial W}+ \frac{\partial E_{2}}{\partial Y_{2}}\frac{\partial Y_{2}}{\partial Y_{1}}\frac{\partial Y_{1}}{\partial Y_{0}}\frac{\partial Y_{0}}{\partial W}$$
- 여기서 마지막항은 0번째 인풋벡터 $X_{0}$가 아웃풋에 미치는 경로를 나타내기도 한다. 그런데 이 경로에 대해서 계산된 그래디언트는 매우 작거나 매우 커질 수 있다. 이는 전형적인 그래디언트 소실/폭주의 문제이다.
- 그런데 RNN에서 그래디언트 소실 문제는 단지 학습이 제대로 안 된다는 것뿐 아니라, 시퀀스를 이루는 인풋 벡터들이 아웃풋에 미치는 영향력의 편차가 의도치 않은 이유로 커진다는 것도 포함한다.
- 가령 아래와 같은 문장이 있을 경우
"로또 1등에 당첨이 되었다. 집값에 얼마 쓰고 부모님 용돈 얼마 드리고 차에 얼마 쓰고 , ... , 에 얼마를 써야 한다."
- 이 문장은 긍정적으로 해석되는 것이 맞다. 로또 1등에 당첨이 되어서 어디에 얼만큼 돈을 쓸지 행복한 고민을 하고 있기 때문이다. 그런데 모델의 입장에서 보면 로또 1등에 당첨이 되었다는 정보는, 이 문장이 긍정적인 감성인지 부정적인 감성인지를 판단하는 아웃풋에서 너무 멀리 떨어져있다. 따라서 그래디언트 계산을 하다보면 로또 1등에 당첨이 되었다는 핵심적인 정보가 가중치 행렬을 업데이트하는 데 기여하는 정도는 매우 작아진다. 반대로 문장 마지막 부분에 돈 쓰는 이야기만 가중치 행렬 업데이트 과정에서 과대반영 되어서 저 좋은 문장을 부정적인 감성으로 판단할 수도 있다.
3.1.2. LSTM Cell
- 이를 해결하기 위해 고안된 아이디어가 바로 LSTM(Long Short-Term Memory)이다. LSTM은 RNN의 셀(노드)를 대체하는데, 다음과 같이 생겼다.

- 복잡하게 생겼다. 하지만 하나씩 뜯어보면 별 것 아니다. 먼저 가장 핵심이 되는 것은 맨 위의 직선인 Cell state이다. Cell state는 정보의 컨베이어 벨트라고 생각하면 된다. LSTM 셀 내에서 여러가지로 조작을 가한 정보들을 Cell state 위에 얹어서 다음 time으로 보내는 것이다.

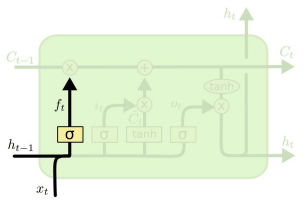
- 나머지 요소들은 그저 주어진 정보들을 어떻게 처리해서 Cell state에 얹을지를 고민하는 것일 뿐이다. 그 중 하나는 망각 게이트(Forget Gate)이다. 망각 게이트는 과거 시점에서 주어진 Cell state 중 얼만큼을 Cell state로 이전할지 결정한다('Cell state'를 잊어버리는 것이다, hidden state나 인풋 벡터를 잊어버리는 게 아니다).
- $\sigma$는 시그모이드 함수인데 0과 1 사이의 값을 가진다. 이는 곧 정보 보존의 비율이며, 1이면 전부 보존하고, 0이면 다 갖다버리라는 뜻이 된다.
- 이때 정보 보존의 비율은 현재 주어진 인풋 벡터와 hidden state의 함수이다. 현재 인풋 벡터와 히든 스테이트를 고려해서, 과거로부터 넘겨 받은 cell state 중 얼만큼을 남기는 게 최적일지 결정하라는 것이다.
- 즉 과거 Cell state 중 얼만큼을 현재 Cell state에 보존할지 그 비중 $f$는 다음의 연산으로 결정된다.
$$f_{t} = \sigma(W_{f} [h_{t-1}, x_{t}] + b_{f})$$
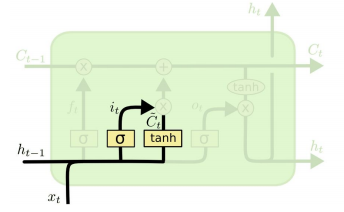
- 두번째 요소는 입력 게이트(Input Gate)이다. 입력 게이트는 망각 게이트와는 반대로 '현재 주어진 인풋벡터와 히든 스테이트' 중 얼만큼을 Cell state에 얹을지를 결정한다. 즉 현재의 새로운 정보에 대한 기억 비중을 결정해준다.
- 기억되는 비중은 현재 인풋벡터와 히든스테이트를 고려하여 계산된 비율인 시그모이드(0과 1 사이의 값)가 된다. 동시에 주어진 정보 자체로부터 특성을 추출해야 하므로 tanh 함수를 거쳐 임시적인 값인 $\tilde{C_{t}}$를 생성한다.
- 그리고 기억될 비중인 시그모이드와, 기억될 정보인 $\tilde{C_{t}}$가 곱해져서 Cell state에 얹어진다.
- 두 가지 게이트를 고려하면, 새로운 Cell state는 다음과 같이 결정된다. C_{t-1}는 과거 정보, \tilde{C_{t}}는 현재 정보를 대변하는 셈이다.
$$C_{t} = f_{t}C_{t-1} + i_{t}\tilde{C_{t}}$$
- 마지막은 출력 게이트(Output Gate)이다. Cell state를 업데이트함과 별개로 현재 값에 대응하는 아웃풋을 반환하고, 다음 기로 넘길 히든 스테이트를 계산하는 것도 당연히 해야 한다. 그림에서는 아웃풋과 히든스테이트가 다르지 않은 것처럼 둘 다 $h_{t}$로 나타냈는데, 실제로는 서로 다른 값이 되도록 할 수도 있다.
- 이때 아웃풋(또는 히든스테이트)은 현재의 인풋과 과거 히든스테이트의 함수로 얻어진 비중 $o_{t}$와 업데이트 Cell state를 고려한 값이 된다. 다시 말해 아래와 같은 연산으로 결정된다.
$$o_{t} = \sigma(W_{o}[h_{t-1},x_{t}] + b_{o})$$
$$h_{t} = o_{t} \, tanh(C_{t})$$
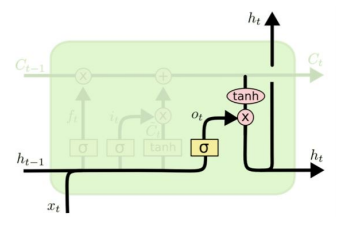
- LSTM cell 내에서 사용되는 많은 파라미터들은 뉴럴넷의 훈련 대상이다.
3.1.3. LSTM과 그래디언트 문제
- LSTM cell을 들여다보면, 정보의 컨베이어 역할을 하는 cell state가 그래디언트 소실/폭주 문제에 기여한다는 것을 알 수 있다. 현재의 cell state 값은
$$C_{t} = f_{t}C_{t-1} + i_{t}\tilde{C_{t}}$$
- cell state에 과거 정보들이 미치는 영향력을 확인하기 위해 임의의 어떤 시점 k(<t)에 대해 편미분하면
$$\frac{\partial C_{t}}{\partial C_{t-1}}*\frac{\partial C_{t-1}}{\partial C_{t-2}}* \, ... \, *\frac{\partial C_{k+1}}{\partial C_{k}}$$
- 이는 다시 쓰면
$$f_{t} * f_{t-1} * \, ... \, * f_{k+1}$$
- 만약 과거 정보가 중요하다고 판단해서 $f_{i}$가 크게 계산되면 그래디언트가 천천히 감소하게 된다. 또한 과거 정보가 아무리 중요하다 하더라도 $f$는 0과 1 사이의 값을 가지므로 그래디언트 폭주가 발생하지도 않는다.
3.2. GRU
- GRU는 LSTM을 보다 간단하게 만든 것이다. 게이트를 통해 기억/망각의 비율을 조절하되 파라미터 수를 최소화하고자 고안되었다. GRU는 다음과 같이 생겼는데, cell state를 없애고 그냥 hidden state를 사용한다.
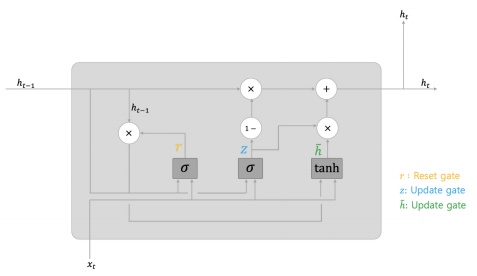
- 기존 hidden state는 reset gate에서 $r$만큼 곱해진 만큼만 반영되도록 한다. 이때 r은 현재 인풋벡터와 기존 히든 스테이트의 가중치 연산된 값에 시그모이드 함수를 먹인 것이다.
$$r_{t} = \sigma (x_{t} W_{r,x} + h_{t-1} W_{r,h} + b_{r})$$
- update gate는 두 개로 나뉘는데 먼저 현재 주어진 정보를 얼마나 반영할지 결정하는 게이트이다. 현재 주어진 정보의 기억 비중인 $z$는 다음과 같이 계산된다.
$$z_{t} = \sigma (x_{t} W_{z,x} + h_{t-1} W_{z,h} + b_{z})$$
- 두번째 update gate는 계산된 비중들을 바탕으로 새로운 hidden state를 업데이트하는 게이트이다.
$$h_{t} = (1-z_{t}) h_{t-1} + z_{t} \tilde{h_{t}}$$
$$\tilde{h_{t}} = tanh(r_{t} W_{t,h} h_{t-1} + W_{t,x} x_{t})$$
4. 실습: RNN 모형을 활용한 주가 예측
- 시계열 포스팅들에서 ARIMA 모델을 가지고 만들었던 주가 예측 모델을 RNN으로 다시 구현해보자.
4.1. 데이터 및 라이브러리 임포트
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from google.colab import drive
drive.mount('/content/drive')
import pandas as pd
data = pd.read_csv('path')
data = data.iloc[:, :2]- 뉴럴넷으로 예측을 할 때는 정상성 가정들을 체크할 필요는 없다. 그러나 스케일링 과정에서 train set의 평균과 표준편차를 계산해야 하는데, 이를 그대로 test set에 적용해야 한다. 주가 시계열은 장기적으로 상승하므로 평균과 표준편차가 변화하는 문제가 있다. 따라서 수익률 시계열을 대신 사용하기로 한다.
data_pr = data.iloc[:]
data_pr['Rate'] = np.log(data['Close']/data['Close'].shift(1))
data_pr = data_pr.dropna()
data_pr.head(5)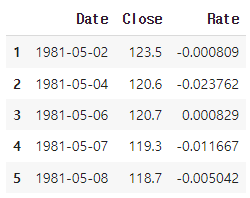
4.2. train set 분리, 스케일링, 텐서화
- 첫 8001 거래일의 데이터를 train set으로 사용한다. 각 인풋(오늘 수익률)에 해당하는 라벨은 내일 수익률이므로, 1일 ~ 8000일이 각각 인풋 벡터가 되고 2일 ~ 8001일이 각각 라벨 벡터가 된다.
- Standard 스케일링을 사용했다.
data_train = data_pr.iloc[:8001, :].reset_index(drop=True)
from sklearn.preprocessing import StandardScaler
scaler_train = StandardScaler()
data_train['Rate'] = scaler_train.fit_transform(data_train['Rate'].to_numpy().reshape(-1, 1))
X_train = data_train.iloc[:8000, :].reset_index(drop=True)
y_train = data_train.iloc[1:8001, :].reset_index(drop=True)- 현재 해결하려는 과제는, 5 거래일 간의 수익률 벡터의 시퀀스를 입력받아서 그 다음날 1일의 수익률을 예측하는 것이다. 따라서 샘플 사이즈 * 시퀀스 길이 * 인풋 벡터 길이의 텐서로 인풋 데이터를 나타내주어야 한다.
def window_slider(df, where_col, sample_size, vec_size, seq_size):
"""
window slider와 tensor화를 동시에 진행
df: 대상 pandas df, where_col: tensor화할 칼럼 인덱스
sample_size: 샘플에 포함되는 날짜 개수, vec_size: 벡터당 길이, seq_size: 시퀀스당 길이
"""
where_col = int(where_col)
sample_size = int(sample_size)
vec_size = int(vec_size)
seq_size = int(seq_size)
mat = np.zeros((sample_size - seq_size + 1, vec_size, seq_size))
for i in range(sample_size - seq_size + 1):
mat[i] = df.iloc[i:seq_size+i, where_col]
output = torch.from_numpy(mat)
output = output.permute(0,2,1)
output = output.to(dtype=torch.float32)
return outputX_train_ws = window_slider(X_train, 2, 8000, 1, 5)
y_train_ws = window_slider(y_train, 2, 8000, 1, 5)
print(X_train_ws[:3, :])
print(X_train_ws[-3:, :])
print(X_train_ws.shape)
4.3. 모델 클래스 구현
# define the RNN model
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(RNN, self).__init__()
self.hidden_size = hidden_size
self.rnn = nn.RNN(input_size, hidden_size, batch_first=True)
self.fc1 = nn.Linear(hidden_size, 10)
self.fc2 = nn.Linear(10, 5)
self.fc3 = nn.Linear(5, 1)
def forward(self, input):
# initialize hidden state
h0 = torch.zeros(1, input.size(0), self.hidden_size)
# pass input through the RNN layer
output, hidden = self.rnn(input, h0)
# pass the output through the fully connected layer
output = self.fc1(F.tanh(output))
output = self.fc2(F.tanh(output))
output = self.fc3(F.tanh(output))
return output# define input and output sizes
input_size = 1
output_size = 1
hidden_size = 20
seq_length = 5
# define the RNN model
rnn = RNN(input_size, hidden_size=hidden_size, output_size=output_size)
# define the loss function and optimizer
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(rnn.parameters(), lr=0.01)4.4. 훈련 및 검증
# train the RNN model
for epoch in range(10000):
optimizer.zero_grad()
# forward pass
outputs = rnn(X_train_ws)
# calculate loss
loss = criterion(outputs, y_train_ws)
# backward pass and optimization
loss.backward()
optimizer.step()
if (epoch+1) % 1000 == 0:
print('Epoch [{}/{}], MSE: {:.4f}'.format(epoch+1, 1000, loss.item()))- 위와 같은 방식으로, 8002 거래일째부터 test set을 만들어 검증한 결과는 아래와 같다.
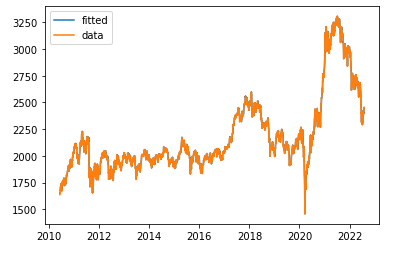
- 먼 스케일에서 보니까 거의 잘 맞추는 것처럼 보인다.
- 예측오차 비율의 제곱 평균의 제곱근은 0.0104 정도로, 오늘 코스피가 2000이라면 오차범위가 위아래로 20p 정도 된다는 뜻이다. 그런데 특별한 것이 없는게, 단순히 어제 주가로 오늘 주가를 예측한 경우에서 동일 지표의 값이 이보다 살짝 작게 나온다.
- 주가가 랜덤워크라는 것을 다시 확인해주는 한편, 이런 기술분석은 큰 의미가 없다는 것을 보여준다. 어제 주가가 이미 오늘 주가에 대한 최선의 추정량이기 때문이다.
'머신러닝&딥러닝' 카테고리의 다른 글
| Deep Learning #6 Attention (0) | 2023.03.02 |
|---|---|
| Deep Learning #5 NLP의 개요 (1) | 2023.02.28 |
| Deep Learning #3 다양한 CNN: VGGNet, GoogleNet, ResNet (0) | 2023.02.22 |
| Deep Learning #2 CNN(합성곱 신경망) (0) | 2023.02.17 |
| Deep Learning #1 딥러닝 기초: 심층신경망의 구조와 간단 코드 실습 (1) | 2023.02.15 |