1. 옵션의 정의
옵션의 정의를 짚고 넘어가자. 옵션이란 기초가 되는 자산(기초자산)을 사전에 약정된 가격(행사가격)으로 매수하거나 매도할 수 있는 권리를 말한다.
1.1. 옵션의 손익 구조
- 콜옵션이란 기초자산의 가격을 만기 시점에 행사가격에 매수할 수 있는 권리이다.
- 기초자산의 만기 시장가격 > 행사가격: 행사가격에 기초자산을 매수하여 시장가격에 매도하면 (시장가격 - 행사가격)만큼의 이득이 발생한다.
- 기초자산의 만기 시장가격 < 행사가격: 행사가격에 기초자산을 매수하여 시장가격에 매도하면 (행사가격 - 시장가격)만큼의 손실이 발생한다. 따라서 이 경우에는 매수 권리를 행사하지 않으므로, 손익이 0이 된다.
만기 시장 가격 $S_{T}$와 행사가격 $K$, 콜옵션 가격 C에 대하여,
콜옵션의 만기 손익
$$ = max(S_{T} - K, 0) - C$$

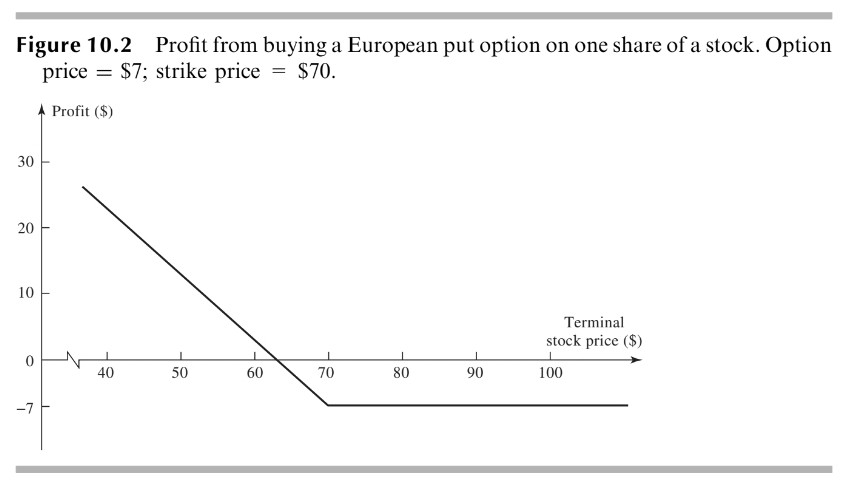
- 풋옵션이란 기초자산의 가격을 만기 시점에 행사가격에 매도할 수 있는 권리이다.
- 기초자산의 만기 시장가격 > 행사가격: 시장가격에 기초자산을 매수하여 행사가격에 매도하면 (시장가격 - 행사가격)만큼의 손실이 발생한다. 따라서 이 경우에는 매도 권리를 행사하지 않으므로, 손익이 0이 된다.
- 기초자산의 만기 시장가격 < 행사가격: 시장가격에 기초자산을 매수하여 행사가격에 매도하면 (행사가격 - 시장가격)만큼의 이득이 발생한다.
만기 시장 가격 $S_{T}$와 행사가격 $K$, 풋옵션 가격 P에 대하여,
풋옵션의 만기 손익
$$ = max(K - S_{T}, 0) - P$$
1.2. 옵션 가격 결정 이론의 의의
옵션의 가격을 잘 구하는 것이 어떤 의미가 있을까? 물론 트레이더들에게는 가격을 잘 책정해서 차익을 남겨야 하니 가격 책정 이론이 의미가 있다. 하지만 블랙-숄즈-머튼이 옵션 가격 결정 이론으로 노벨상까지 받은 데에는 그보다 더 근본적인 이유가 있다.
옵션은 모든 파생상품(은 결국 금융상품의 일반화된 개념이다)을 구성하는 기본요소(Building Block)라고 말할 수 있다. 가령 선물(Future)의 매수 포지션은 콜옵션 매수와 풋옵션 매도 포지션의 합으로 복제할 수 있다. 뿐만 아니라 우리가 상상할 수 있는 대개의 파생상품의 포지션들은 여러 옵션들을 적당하게 합성함으로써 복제할 수 있다. 예컨대 버터플라이(Butterfly)라고 부르는 아래의 포지션은 시장의 변동성이 낮은 시기에, 가격이 너무 뛰거나 내리지 않기만 하면 이득을 보는 포지션이다. 이는 복수의 행사가격을 가진 풋옵션의 매수/매도 포지션의 합성으로 복제할 수 있다.

이것 외에 다양한 응용이 가능하다. 예컨대 채권은 기업이 부도가 발생할 경우 기업의 잔존가치만큼을 돌려받고, 부도가 발생하지 않을 경우 고정된 액면가격을 돌려받는 상품이다. 이는 풋옵션의 매도 포지션으로 복제할 수 있다. 보험상품도 마찬가지이다. 보험사 입장에서 화재보험은 화재가 발생할 경우 보험금 지출이 발생하고 그렇지 않으면 보험료 수입이 발생하는 금융상품이다. 화재보험은 주식이나 채권, 외환의 가격이 아니라 화재 발생 여부를 정의역으로 하여 현금흐름을 매핑하는 함수일 뿐인 것이다.
파생상품은, 거래할 당사자만 있다면 상상할 수 있는 모든 화폐적/비화폐적 사건들로부터 현금흐름을 창출한다. 파생상품은 단지 화폐적 이득과 손실로 대변되는 천박한 세계를 대변하는 것이 아니라, 인간이 직면하는 불확실한 세계에 대응하는 하나의 방법이다. 그리고 모든 파생상품의 기초가 되는 옵션의 가격을 정확하게 책정할 수 있다는 것은 인간이 직면하는 모든 불확실성들은 가격을 매겨 시장 거래를 통해 대비할 수 있다는 의미이다. 이러니 재미가 없을 수가 있는지... 파생상품 이론은 단지 '돈'에 대한 공부가 아니다.
<Reference>
Hull, J. C. (2015) "Options, Futures, and Other Derivatives" (9th Edtion)
'파생상품&금융공학' 카테고리의 다른 글
| 파생상품 이론 #3 선물을 활용한 헷징 전략 (5) | 2023.01.19 |
|---|---|
| 파생상품 이론 #2 선물시장의 이해 (0) | 2023.01.18 |
| Black-Scholes-Merton Model #3: BSM 모델의 검증(Python 예제) (1) | 2023.01.15 |
| 파생상품 이론 #1 파생상품의 정의와 시장 구조 (0) | 2023.01.15 |
| Black-Scholes-Merton Model #2: 옵션 가격의 해석적 해(Analytic Solution) (0) | 2023.01.10 |