파생상품 가치평가 방법론 #9 유한차분법(FDM) 구현하기

이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크

Options, Futures, and Other Derivatives

 

이전 글: FDM의 아이디어

 

파생상품 가치평가 방법론 #8 유한차분법(FDM)의 아이디어

---

1. 경계 조건 이용하기

 

암묵적 유한차분법에서 node (i, j)에서의 파생상품 가치는 다음과 같다.

$$f_{i,j} = \alpha_{j}*f_{i-1,j-1} + \beta_{j}*f_{i-1,j} + \gamma_{j}*f_{i-1,j+1}$$

 

유한차분법에서는 각 node의 파생상품 가치가 만족해야 할 위의 미분방정식을 통해서 원하는 node의 파생상품 가치를 구한다. 그런데 문제가 하나 있다. 우리는 어떤 node (i,j)에서도 파생상품의 가치를 모르는데, 어떻게 원하는 node에서의 가치를 구할 수 있을까?

 

파생상품의 성질을 이해하면, 우리는 일부 node에서는 파생상품의 가격을 확실하게 알 수 있다. 첫째, 만기에서는 파생상품의 가치를 확실하게 알 수 있다. 만약 행사가격이 K인 콜옵션이라면, 만기 시점 T = N*dt에서 콜옵션의 가치는 $$f_{N, j} = max(S_{N, j} - K, 0)$$

 

둘째, 기초자산 가격이 0이면 이때 콜옵션의 가치는 0에 수렴한다고 가정할 수 있다. 물론 현실에서 기초자산 가격이 0이라고 해서 꼭 콜옵션 가치가 0인 것은 아니다. 왜냐하면 잔존만기 동안 기초자산 가격이 높아질 여지도 있으니까. 하지만 우리는 콜옵션 가치가 0이 된다고 가정한다. 셋째, 유사한 이유로 아주 충분히 큰 기초자산 가격 $S_{max}$에서는 콜옵션 가치가 행사가치의 현재가치로 주어진다고 가정한다. 즉 임의의 시점 t = i*dt에서,

$$f_{i, 0} = 0$$

$$f_{i, M} = max(S_{max} - Ke^{-r(T-t)}, 0)$$ 

 

그럼 우리는 아래의 grid에서 최상단과, 최하단, 그리고 우극단의 세 경계에서 파생상품 가치를 알고 있는 셈이다.

 

 

2. Backwardation 알고리즘

 

그럼 만기 시점의 값을 알고 있으니까, 만기보다 한 시점 전에서 파생상품의 가치를 결정해보자.

주어진 시점 t = (N-1)dt에서, 기초자산 가격 상태가 0부터 5까지라고 하자(즉 기초자산 가격의 최대값이 5).

 

우선 t시점에서 가격이 0일 때와 5(최대값)일 때 파생상품 가격은 알고 있다.

$$f_{N-1, 0} = 0$$

$$f_{N-1, 5} = V_{N-1,5} = max(S_{max} - Ke^{-r(T-t)}, 0) $$

 

우리가 모르는 4개의 가격을 구하기 위해, 시점만 1시점 후로 옮겼을 때의 방정식을 정리해보자.

$$f_{N, 1} = \alpha_{1}f_{N-1,0} + \beta_{1}f_{N-1,1} + \gamma_{1}f_{N-1,2}$$

$$f_{N, 2} = \alpha_{2}f_{N-1,1} + \beta_{2}f_{N-1,2} + \gamma_{2}f_{N-1,3}$$

$$f_{N, 3} = \alpha_{3}f_{N-1,2} + \beta_{3}f_{N-1,3} + \gamma_{3}f_{N-1,4}$$

$$f_{N, 4} = \alpha_{4}f_{N-1,3} + \beta_{4}f_{N-1,4} + \gamma_{4}f_{N-1,5}$$

 

이때 좌변의 값들은 이미 알고 있는 값들이다. 만기 시점 가격이기 때문이다. 또한 $f_{N-1,0}$과 $f_{N-1, 5}$도 알고 있는 값이다. 우리가 알고 있는 값들을 좌변으로 밀어넣자.

$$f_{N, 1} - \alpha_{1}f_{N-1,0} = \beta_{1}f_{N-1,1} + \gamma_{1}f_{N-1,2}$$

$$f_{N, 2} = \alpha_{2}f_{N-1,1} + \beta_{2}f_{N-1,2} + \gamma_{2}f_{N-1,3}$$

$$f_{N, 3} = \alpha_{3}f_{N-1,2} + \beta_{3}f_{N-1,3} + \gamma_{3}f_{N-1,4}$$

$$f_{N, 4} - \gamma_{4}f_{N-1,5} = \alpha_{4}f_{N-1,3} + \beta_{4}f_{N-1,4}$$

 

행렬 방정식 형태로 표현하면, 문제가 명확해진다.

 

$$\begin{pmatrix} f_{N, 1} - \alpha_{1}f_{N-1,0} \\f_{N, 2}\\ f_{N, 3} \\ f_{N, 4} - \gamma_{4}f_{N-1,5} \end{pmatrix} = \begin{pmatrix} \beta_{1} & \gamma_{1} & 0 & 0 \\ \alpha_{2} & \beta_{2} & \gamma_{2} & 0 \\0 & \alpha_{3} & \beta_{3} & \gamma_{3} \\ 0 & 0 & \alpha_{4} & \beta_{4} \end{pmatrix} \begin{pmatrix} f_{N-1, 1} \\f_{N-1, 2}\\ f_{N-1, 3} \\ f_{N-1, 4}\end{pmatrix}$$

 

우변의 벡터가 우리가 알고자 하는 (N-1)dt 시점의 파생상품 가격 벡터이다. 우변의 파라미터 행렬의 역행렬을 취해서 좌변으로 넘겨주면 된다. 

 

이렇게 해서 만기 직전 시점의 가격을 구하면, 그 이전 시점의 가격도 마찬가지로 역행렬 방법으로 구할 수 있다. 반복하여 초기 시점의 파생상품 가격도 구할 수 있다.

 

3. 코드 구현

코드로 구현한 결과는 아래와 같다. 행사가격 50, 무위험이자율 5%, 변동성 20%, 만기 5년인 콜옵션이다. 잔존만기는 각각 0.25년의 길이를 갖도록 분할하였고, 기초자산 가격은 5의 길이를 가지도록 분할하였다. 가격 최대값은 100으로 설정하였다. 

 

def BSM_call(S, K, r, T, t, s):
  d1 = (np.log(S/K) + (r + 1/2 * s**2) * (T-t)) / (s * np.sqrt(T-t))
  d2 = d1 - s * np.sqrt(T-t)
  N_d1 = norm.cdf(d1)
  N_d2 = norm.cdf(d2)
  call = S * N_d1 - K * np.exp(-r*(T-t)) * N_d2
  return call

def Linear_interpolation(value, underlying, target_underlying):
  index_0 = np.where(underlying <= target_underlying)[-1][-1]
  index_1 = np.where(underlying >= target_underlying)[0][0]
  value_0 = value[index_0]
  value_1 = value[index_1]
  underlying_0 = underlying[index_0]
  underlying_1 = underlying[index_1]
  if value_0 == value_1:
    return value_0
  else:
    return value_0 + (value_1 - value_0)/(underlying_1 - underlying_0) * (target_underlying - underlying_0)

S0 = 50; K = 50; r = 0.05; s = 0.20
dt = 0.25; T = 5
S_max = 100; dS = 5

J = int(S_max / dS); I = int(T/dt)

Grid_underlying = np.zeros([J+1, I+1]) #기초자산가격 0부터 S_max까지 J번 점프하므로 총 J+1개의 가격, 시간은 0부터 T까지 I번 점프하므로 총 I+1개의 시점
for j in np.arange(J+1):
  for i in np.arange(I+1):
    Grid_underlying[j, i] = j * dS

Grid_coef = np.zeros((J-1, 3)) #(a1, b1, c1)부터 (aJ-1, bJ-1, cJ-1)까지 J-1개의 파라미터
for j in np.arange(1,J,1): #1부터 J-1까지의 index
  a = 1/2 * r * j * dt - 1/2 * (s**2) * (j**2) * dt
  b = 1 + (s**2) * (j**2) * dt + r * dt
  c = -1/2 * r * j * dt - 1/2 * (s**2) * (j**2) * dt
  Grid_coef[j-1,:] = np.array((a,b,c)) #for문 index가 1부터 시작했으므로 행렬 index 기준으로는 1-1 = 0번부터 채워줌

Matrix_coef = np.zeros((J-1, J-1)) #가격이 0일때와 S_max일 때를 제외하면 J-1 * J-1 행렬
Matrix_coef[0, :2] = Grid_coef[0, 1:] #첫 행은 1, 2번째 원소에 b1, c1
Matrix_coef[J-2, -2:] = Grid_coef[J-2, :-1] #J-1행은 -2, -1번째 원소에 aJ-1, bJ-1
for j in np.arange(1, J-2, 1): #2번째 행부터 J-2번째 행까지
  Matrix_coef[j, j-1:j+2] = Grid_coef[j] #j번째 행에서,

Inverse_coef = np.linalg.inv(Matrix_coef)

Grid_value = Grid_underlying.copy()
Grid_value[0,:] = 0
Grid_value[:,-1] = np.maximum(Grid_value[:,-1] - K, 0)
for i in np.arange(I):
  Grid_value[-1,i] = np.maximum(Grid_underlying[-1,i] - K*np.exp(-r*(T-i*dt)), 0)

a = Grid_coef[0,0]
c = Grid_coef[J-2,2]
for i in np.arange(I-1,-1,-1):
  Matrix_value = Grid_value[1:-1,i+1].copy()
  Matrix_value[0] = Matrix_value[0] - a * Grid_value[0,i]
  Matrix_value[J-2] = Matrix_value[J-2] - c * Grid_value[J,i]
  Iteration = Inverse_coef @ Matrix_value.reshape(J-1,-1)
  Grid_value[1:-1,i] = Iteration.reshape(J-1)

result = Linear_interpolation(Grid_value[:, 0], Grid_underlying[:, 0], S0)
print(result)

 

 

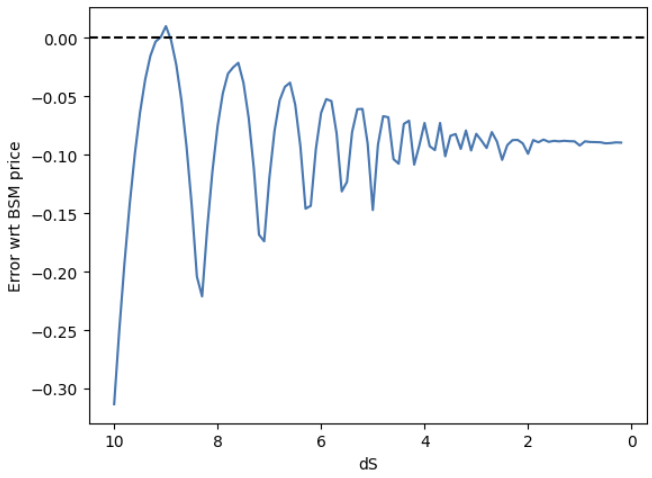
구한 가격은 14.425이고 BSM 가격은 14.569으로 대략 0.13의 오차가 있었다. 가격 구간을 더 잘게 쪼갤 경우 수렴성을 테스트해보면, 가격 구간의 길이가 0에 가까워질수록 BSM 가격과의 오차가 약 0.1 정도로 수렴한다.