이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크
Options, Futures, and Other Derivatives
ISBN-13: 9780136939917 Options, Futures, and Other Derivatives Published 2021
www.pearson.com
10편
파생상품 이론 #10 옵션의 Greeks
이 시리즈는 파생상품 이론 분야에서 가장 유명한 교재인 Hull(2021)의 "Options, Futures and Other Derivatives (11th)"을 요약한 것일 뿐이다. 아래는 책 구매 링크 Options, Futures, and Other Derivatives ISBN-13: 978013693
seungbeomdo.tistory.com
1. 콜옵션과 풋옵션의 내재변동성
- 이전 포스팅에서 다루었듯이, 내재변동성(Implied Volatility)이란 BSM 모델의 가정 하에서 주어진 옵션 가격으로부터 얻어낸 기초자산 수익률의 변동성이다.
- 그런데 옵션은 콜옵션과 풋옵션 두 종류가 있기 때문에 기초자산, 만기, 행사가격 등 여타의 조건들이 동일하더라도 두 옵션의 내재변동성이 다를 수도 있다는 의문이 들 것이다. 하지만 결론부터 말하면 콜옵션과 풋옵션의 내재변동성은 항상 동일하다.
- 이를 증명하기 위해서 풋-콜 패리티 조건을 사용한다(마찬가지로 이전 포스팅에서 다루었다). 풋-콜 패리티는 BSM 가정 하에서만 성립하는 것은 아니다. 단지 무위험 차익거래가 존재하지 않는다는 조건만 있다면 항상 성립한다. 다음의 식이다.
$$P_{mkt} + S_{0}e^{-qT} = C_{mkt} + Ke^{-rT}$$
- 하첨자 mkt는 시장에서 관측된 가격임을 의미한다. 풋-콜 패리티는 무위험 차익거래가 존재하지 않는다는 가정 하에서는 항상 성립하므로, BSM 모형 하에서의 해석적 해에 대해서도 당연히 성립한다. 여기서의 하첨자 BSM은 BSM 모델의 해석적 해라는 것을 뜻한다.
$$P_{BSM} + S_{0}e^{-qT} = C_{BSM} + Ke^{-rT}$$
- 아래 식에서 위의 식을 빼면 다음과 같다.
$$P_{BSM} - P_{mkt} = C_{BSM} - C_{mkt}$$
- 주어진 풋옵션에 대해서, 시장의 내재변동성과 BSM 모델에서 사용한 변동성이 일치한다고 가정하자. 그러면 $P_{BSM} = P_{mkt}$이므로 좌변이 0이 되어 우변도 0이어야 한다. 즉 $C_{BSM} = C_{mkt}$이다. 그리고, BSM 모델에서 사용하는 변동성은 콜옵션과 풋옵션에 대하여 동일해야 한다.
- 두 논의를 결합하면, 시장에서 관측된 풋옵션의 내재변동성은 콜옵션의 내재변동성과 같아야 한다.
2. 변동성 미소(Volatility Smile)
2.1. 변동성 미소의 개념
- 변동성 미소란, 특정한 옵션의 내재변동성을 행사가격/기초자산가격 비율의 함수로 표현한 것이다. X축을 행사가격, Y축을 내재변동성으로 나타낼 때, 그래프는 일반적으로 원점에 대해 볼록한 형태를 갖는다. 그래서 변동성 미소라고 부른다.

- 1장에서 살펴보았듯이, 콜옵션과 풋옵션의 내재변동성은 동일해야 하므로, 변동성 미소를 논의할 때 주어진 옵션이 콜인지 풋인지는 고려하지 않아도 된다.
2.2. 변동성 미소와 내재분포
- 옵션의 내재분포(Implied Distribution)란, 옵션 가격으로부터 유도해낸 기초자산 가격의 확률분포를 뜻한다. 구체적인 유도과정은 다른 포스팅에서 다룬다(https://seungbeomdo.tistory.com/51).
- 옵션의 내재변동성이 볼록한 그래프 형태를 가질 때, 기초자산 가격에 대한 내재분포는 로그정규분포(Log-Normal distribution)보다 두꺼운 꼬리(Fat-tailed distribution)를 갖는다.

- 어떤 콜옵션이 있는데, 현재 콜옵션의 기초자산가격이 행사가격보다 매우 낮은(Deep OTM) 상태라고 하자. 이때 옵션의 가격은 로그노말분포를 가정했을 때보다, 두꺼운 꼬리 분포를 가정했을 때 더 높을 것이다.
- 왜냐하면 Deep OTM 콜옵션이 행사되려면 기초자산가격이 매우 높아져야 하는데, 두꺼운 꼬리 분포가 바로 그런 특성을 가지기 때문이다.
- 마찬가지로 현재 기초자산가격이 행사가격보다 매우 높은 풋옵션을 생각하자. 이때에도 옵션의 가격은 두꺼운 꼬리 분포를 가정했을 때 더 높다. 왜냐하면 Deep OTM 풋옵션이 행사되려면 기초자산가격이 매우 낮아져야 하는데, 두꺼운 꼬리 분포가 그런 특성을 갖는다.
- 그리고 두꺼운 꼬리 분포 하에서 Deep OTM 옵션의 가격이 더 높다는 것은, K/S의 값이 양쪽으로 극단적일 때 옵션의 내재변동성이 더 높다는 것을 의미한다. 따라서 변동성 미소가 나타나는 상황에서는 기초자산 가격의 내재분포가 두꺼운 꼬리를 갖는다.
3. 통화옵션과 주식옵션의 변동성 미소
3.1. 통화옵션의 변동성 미소
- 실증적으로 통화옵션에서는 변동성 미소가 관찰된다는 것에는 어느정도 합의가 이루어져 있다.

- 이는 환율의 내재분포가 로그노말분포보다 두꺼운 꼬리를 갖는다는 것을 의미한다.

- 통화옵션에서 변동성 미소가 존재하는 이유는 무엇일까? 달리 말해 환율이 로그노말분포를 따르지 않는 이유는 무엇일까? 어떤 자산가격이 로그노말분포를 따르기 위해서는 두 가지의 조건이 필요하다.
- 자산가격의 변동성이 일정하다.
- 자산가격이 점프하지 않고 연속적으로 변화한다.
- 쉽게 짐작할 수 있듯이, 환율의 변동성은 상수가 아니고, 외환시장의 충격에 의해 점프가 종종 발생한다. 따라서 환율이 로그노말분포를 따를 것이라는 기대는 현실적으로 어렵다.
- 한편 변동성이 변화하는 경우 옵션가격에 미치는 영향력은 옵션만기가 증가함에 따라 커지고, 점프가 가격에 미치는 영향은 옵션만기가 증가함에 따라 작아진다.
- 전자는 옵션만기가 길 때, 증가하는 변동성은 옵션의 기대 행사가치를 높이기 때문이다.
- 후자는 옵션만기가 길 때, 양방향으로의 점프가 서로 상쇄되기 때문이다.
3.2. 주식옵션의 변동성 미소
- 주식옵션에도 변동성 미소가 존재한다는 것이 잘 알려져있다. 그런데 주식옵션의 경우에는 통화옵션과는 조금 다른 형태의 변동성 미소를 갖는다. 우하향하는 기울기의 변동성 미소를 갖는데, 이를 Volatility Skew라고 부르기도 한다.
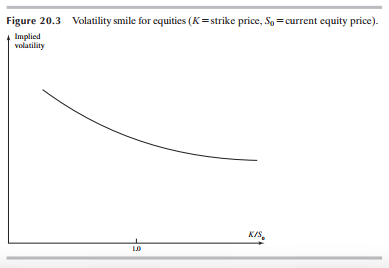
- 주가가 낮아질수록 혹은 행사가격이 높아질수록 주가수익률의 내재변동성이 작아진다는 것을 의미한다. 이는 또한 다음과 같은 형태의 내재분포를 의미한다. 오른쪽으로는 얇은 꼬리를, 왼쪽으로는 두꺼운 꼬리를 갖는 내재분포이다.
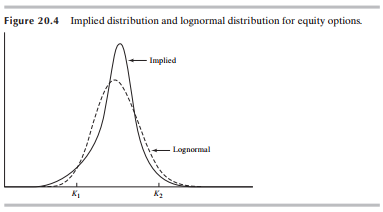
- 주가가 행사가격보다 매우 낮은, Deep OTM 콜옵션을 생각해보자. 이 콜옵션의 내재분포가 오른쪽으로 짧은 꼬리를 가질 경우 로그노말인 경우보다 행사될 확률이 더 낮다. 이는 이 콜옵션의 가격을 낮추고, 수익률의 내재변동성이 낮아지도록 하는 상황을 의미한다.
- 동시에 주가가 행사각격보다 매우 높은, Deep OTM 풋옵션을 생각해보자. 이 풋옵션의 내재분포가 왼쪽으로 긴 꼬리를 가질 경우 로그노말인 경우보다 행사될 확률이 더 높다. 이는 이 풋옵션의 가격을 높이고, 수익률의 내재변동성이 높아지도록 하는 상황을 의미한다.
- 왜 주가는 이런 형태의 내재분포를 가질까? 일반적으로 주가와 변동성은 음의 상관을 가진다. 주가가 내려가면 변동성이 높아지고 주가가 높아지면 변동성이 낮아지는 경향이 있다.
- 따라서 주가가 높아질 때는 변동성이 낮아져서, 극단적인 주가 상승이 발생하는 경우는 많지 않다. 따라서 오른쪽으로는 짧은 꼬리를 갖는다, 주가가 낮아질 때는 변동성이 높아져서, 극단적인 주가 하락이 발생하는 경우는 상대적으로 빈번하다. 따라서 왼쪽으로 긴 꼬리를 가지게 된다.
3.3. 쌍봉분포를 갖는 경우의 변동성 미소
- 조금 더 특수한(혹은 현실적인) 경우로서, 자산시장에 어떤 결정적인 이벤트가 존재하여, 기초자산의 가격이 쌍봉분포(Bimodal Ditribution)를 갖는 경우를 생각해보자. 가령 제약회사의 임상시험 통과 여부, M&A 체결 여부 등등이 발생하면 그 결과에 따라서 크게 차이가 나기 때문에 아래와 같은 내재분포가 형성된다.
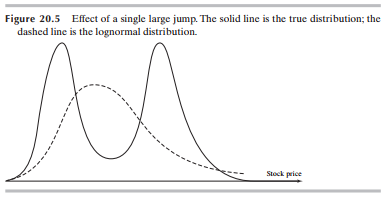
- 이 경우의 변동성 미소는 오목한 형태를 가질 것이다. 따라서 이 경우는 Volatility Frown이라고 부르기도 한다.
4. 변동성 표면(Volatility Surface)
- 변동성 표면이란, 옵션의 내재변동성을 행사가격/기초자산가격의 비율과, 잔존만기의 두 가지 변수의 함수로 나타낸 것을 말한다. 내재변동성과 잔존만기의 관계는 변동성의 기간구조(Term Structure)라고 부르기도 한다.
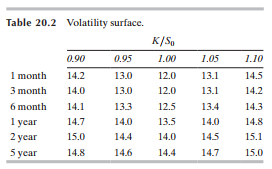
- 변동성 표면을 보면, 일반적으로 짧은 만기 하에서 변동성 미소가 선명하고, 긴 만기에서는 변동성 미소가 흐릿해지는 경향이 있다. 동시에 내재변동성의 수준 자체는 잔존만기가 길수록 높아진다.
5. 최소분산 델타
- 변동성 미소의 존재를 고려하면, 옵션의 헷징 델타는 다소 수정돼야 할 필요가 있다. 왜냐하면 옵션의 헷징 델타는 기초자산 가격 변화에 대한 옵션 가격의 변화율을 나타내는데, 기초자산 가격이 변화하면 내재변동성이 변화해서 옵션 가격에 추가적인 변화가 발생하기 때문이다.
- 이를 고려한 헷징 델타는 다음과 같다.
$$\Delta_{MV} = \frac{\partial f_{BSM}}{\partial S} + \frac{\partial f_{BSM}}{\partial {\sigma}_{imp}} \frac{\partial E[\sigma_{imp}]}{\partial S}$$
- 이를 다시 쓰면,
$$\Delta_{MV} = \Delta_{BSM} + \mathcal{V}_{BSM} \frac{\partial E[\sigma_{imp}]}{\partial S}$$
- 이때 주가에 대한 변동성의 편미분은 음수이고, BSM 모델에서 베가는 양수이기 때문에 수정된 델타는 기존 델타보다 작은 값이다.
'파생상품&금융공학' 카테고리의 다른 글
| 파생상품 이론 #12 Value-at-Risk & Expeceted Shortfall (0) | 2023.03.03 |
|---|---|
| 옵션가격의 내재분포(Implied Distribution) (1) | 2023.03.02 |
| 파생상품 이론 #10 옵션의 Greeks (0) | 2023.02.24 |
| 파생상품 이론 #9 Black-Scholes-Merton 모형 (0) | 2023.02.21 |
| 파생상품 이론 #8 이항모형 (0) | 2023.02.14 |