1. 차원 축소(Dimensionality Reduction)
- 대부분 데이터 분석의 궁극적인 목표는 종속변수 $Y$를 일련의 독립변수 집합 $[X_{1}, X_{2}, ... , X_{n}]$으로 설명하는 것이다. 그런데 이때 사용하는 독립변수 벡터의 차원이 너무 많으면 여러가지로 문제가 발생한다.
- 불필요한 혹은 다른 변수들과 유의한 차이가 없는 독립변수들이 포함되면 모형의 성능이 저하된다.
- 너무 많은 독립변수들을 고려하다보니 계산 비용이 증가한다.
- 비전문가에게 분석 결과를 이해시키는 직관적인 방법은 시각화인데, 변수 공간이 3차원 이상이 되면 시각화를 하기가 매우 어렵다.
- 따라서 모형이 사용할 독립변수들을 줄이는 것은 매우 중요한 과제라고 하겠다. 이때 독립변수 벡터의 차원을 줄인다고 해서, 이 과정을 차원 축소라고 부른다.
- 그런데 차원 축소를 아무렇게나 해서는 안 된다. 두 가지의 상충하는 목표가 있다.
- 최대한 적은 수의 독립변수들만을 사용할 것
- 그러면서도 원래의 샘플의 특성을 잘 살릴 수 있도록 할 것
2. 특성 추출 기법
- 차원 축소에는 두 가지 유형이 있다. 하나는 중요한 특성들만을 뽑아서 사용하는 것이고, 다른 하나는 특성들의 결합을 통해, 보다 많은 정보량을 집약하는 독립변수를 새로 생성하는 것이다. 전자를 먼저 살펴보도록 하자.
2.1. Forward Selection: mRMR
- 중요한 독립변수들을 순서대로 하나씩 뽑는 특성 추출 기법을 Forward Selection이라고 한다. 대표적인 방법은 mRMR(minimum redundancy maximum relevance)이다.
- 알고리즘을 설명하면 다음과 같다.
- 먼저 주어진 독립변수 집합 $F$로부터 몇 개의 독립변수를 뽑을 것인지 정해준다.
- 둘째, 독립변수들과 종속변수의 상관계수를 구하여 절대값이 가장 큰 독립변수를 첫번째로 선택한다.
- 셋째, 추출된 독립변수들의 집합을 $S$라고 하고, 원 집합 $F$를 선택된 독립변수를 제외한 집합으로 재정의한다.
- 넷째, 그 다음부터는 종속변수 $Y$와 상관계수가 가장 높으면서 동시에 기존에 선택된 독립변수 집합 $F$와의 평균적인 상관계수가 가장 낮은 것으로 정한다. 즉 새롭게 선택되는 독립변수 $X_{*}$는 다음의 조건을 만족한다.
$$X_{*} = argmax_{X_{i} \in F} \{|corr(X_{i}, Y)| - \frac{1}{|S|} \Sigma_{X_{j} \in S} |corr(X_{i}, X_{j})| \}$$
- 미리 지정해둔 $k$개의 독립변수들이 선택될 때까지 이 과정을 반복한다.
- mRMR의 장점은 아이디어가 직관적이라는 것이고, 단점은 선형 연관성인 상관계수만을 사용하므로 비선형적 연관은 반영하지 못한다는 것이다.
2.2. Backward Elimination: SVM-RFE
- 두번째 특성추출 방법은 불필요한 독립변수들을 순서대로 제거해나가는 것이다. 대표적인 예는 SVM-RFE이다. 이름에서도 알 수 있듯이 SVM을 사용해서 불필요한 변수가 무엇인지 찾아낸다.
- 알고리즘을 설명하자면 다음과 같다.
- 먼저 전체 독립변수들을 가지고 $Y$를 분류하는 SVM을 생성한다.
- 둘째, SVM은 어떤 독립변수들이 갖는 영향력을 계산할 수 있으므로 추정된 SVM으로부터 가장 영향력이 낮은 독립변수를 제거한다.
- 원하는 독립변수 개수 $k$에 도달할 때까지 위 과정을 반복하면서 불필요한 독립변수들을 제거한다.
- SVM은 다양한 커널 함수들을 사용해서 비선형적 구분까지 가능하다. 따라서 SVM-RFE는 비선형적 연관까지 반영할 수 있다는 장점이 있다. 단점은 어떤 커널 함수를 사용해야할지부터 해서 조정해야 할 파라미터가 많다는 것이고 SVM을 매번 훈련해야 하기 때문에 계산 비용이 크다는 것이다.
3. Feature Extraction
- 차원 축소를 진행하는 또다른 큰 분류는(그리고 일반적으로 사랑 받는 방법은) 특성 추출이다. 이는 기존의 독립변수들을 적당하게 조합하여 새로운 독립변수들을 사용하는 것이다. 즉 더 많은 정보를 집약하고 있는 소수의 독립변수들을 새로 만들어내겠다는 뜻이다.
3.1. 주성분 분석(PCA)
- PCA는 주어진 변수들의 선형결합(Linear Combination)을 통해서 새로운 변수를 생성한다. 원래 주어져있던 독립변수 집합 $[X_{1}, X_{2}, ... , X_{n}]$로부터 다음과 같은 변수 $Z$를 찾는 것이다. 이를 주성분이라고도 한다.
$$Z =w_{1}X_{1} + w_{2}X_{2} + ... + w_{n}X_{n}$$
- 이때 중요한 아이디어는 새롭게 생성된 변수가 분산이 크면 클수록 좋다는 것이다.
- 왜 분산이 클수록 좋을까? 분산이 크다는 것은 변별력이 높다는 것을 의미하기 때문이다. 국어 성적은 학생들이 고만고만하게 다들 잘 받지만 수학 성적은 학생마다 편차가 크다. 따라서 학생들의 총 성적을 변별하는 중요한 과목은 수학이다.
- PCA의 알고리즘은 다음과 같다. 첫째, 주어진 독립변수들의 선형결합 중 분산이 가장 커지는 선형결합을 생성한다. 이는 분산을 극대화하는 계수 벡터 $[w_{1}, w_{2}, ... , w_{n}]$을 찾는다는 뜻이다.
$$argmax_{[w_{1}, w_{2}, ... , w_{n}]} Var(Z)$$
subject to $\Sigma^{n}_{i=1} w_{i}^{2} = 1$
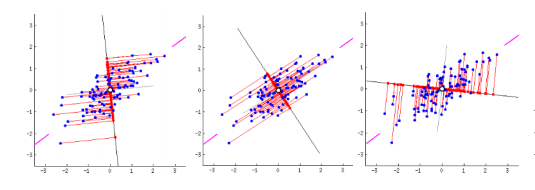
- 선형결합을 찾는다는 것의 의미를 기하학적으로 조금만 고찰해보자. 아래 그림에서 파란 점들은 샘플을 의미한다. 3개의 그림들에서 샘플들의 분포는 모두 기존 ($X$, $Y$) 좌표 체계에서는 동일하다.
- $X$와 $Y$의 임의의 선형결합은 각 그림에서 샘플들을 가로 지르는 붉은 직선을 의미한다. 새로운 주성분이 만들어지면 이 붉은 직선이 새로운 좌표축(새로운 변수)이 된다.
- 그리고 각각의 좌표축으로 샘플들을 사영시켰을 때, 좌표축 상에서 샘플들이 보이는 분산은 모두 다를 것이다. PCA는 바로 그 분산을 최대화하는 선형결합(즉 새로운 축)을 찾는다.
- 조건을 만족하는 계수 벡터의 해석적 해는 Lagrangian 방법으로부터 다음과 같이 주어져있다. 독립변수 벡터의 공분산 행렬 $S$에 대하여 다음을 만족하는 벡터 $w$가 우리가 찾는 계수 벡터이다. 즉 공분산 행렬의 고유벡터이다.
$$Sw = \lambda w$$
- 둘째, 이렇게 추출된 계수 벡터와 직교하면서(공분산 = 0) 분산이 가장 큰 계수 벡터가 우리가 찾는 두 번째 계수 벡터가 된다. 직교를 해야하는 이유는 기존에 생성된 주성분과 상관이 적은 주성분을 찾고자 하기 때문이다.
- 이 과정을 반복하면서 우리가 원하는 새로운 특성변수 $[Z_{1}, Z_{2}, ... , Z_{n}]$를 구한다. 이때 생성된 주성분의 개수는 원 독립변수의 차원과 동일하다. 이들 중에서 상위 몇 개만 뽑아서 사용하면 차원축소가 된 셈이다.
- 한편, 위에서 적은 고유벡터의 해는 주어진 공분산 행렬에 대해 유일하지 않다. 각각의 고유벡터들을 대응하는 고유값의 크기 순서로 줄 세워서 $k$개를 뽑는 것이 결국 주성분 $k$개를 뽑는 것과 같다.
3.2. LDA(Linear Discriminant Analysis)
- 두번째로 소개할 특성 추출 기법은 LDA이다. LDA는 PCA와 마찬가지로 기존 독립변수들의 선형결합을 찾아 새로운 독립변수드를 생성한다. 차이점은, PCA는 $Y$값을 고려하지 않고 그냥 생성된 주성분의 분산이 크도록 하는 계수 벡터를 찾는 것이었지만, LDA는 $Y$값도 고려해서 그것들을 찾는다는 데 있다.
- 따라서 LDA는 $Y$의 라벨이 주어진 상태에서 $Y$를 잘 구분할 수 있는 주성분을 생성한다고 생각하면 된다. $Y$를 잘 구분한다는 것은 다음의 아이디어로 구체화된다. 첫째는 새로운 주성분 벡터의 클래스 내 거리(Within-Class-Distance)를 최소화하는 것이고 둘재는 새로운 주성분 벡터의 클래스 간 거리(Between-Class-Distance)는 최대화하는 것이다.
- 클래스 간 거리는 각 클래스의 중심점으로부터의 거리를 의미하고, 클래스 내 거리는 각 클래스의 샘플들의 중심점으로부터 거리를 의미한다. 두 클래스의 중심점을 $m_{1}$, $m_{2}$라고 하고 각 클래스의 중심점-표준편차를 $s_{1}$, $s_{2}$라고 하면 구하고자 하는 계수벡터 $w$는 다음과 같다.
$$argmax_{w} \frac{(m_{2} - m_{1})^2}{s_{1}^{2} + s_{2}^{2}}$$
3.3. MDS(Multi Dimensional Scaling)
- 다차원 척도법도 선형결합을 통해 주성분을 찾아내는 방법이지만, $Y$값을 고려하지 않는다는 점에서 LDA와는 구분된다. 동시에 분산 최대화 기준을 사용하지 않고 다른 기준을 사용해 최적의 주성분을 찾아낸다는 점에서 PCA와도 구분된다.
- MDS가 사용하는 기준은 원래의 변수 공간에서 샘플 간의 거리 관계가 최대한 보존되도록 하자는 것이다. 즉 생성된 주성분을 축으로 하는 새로운 변수 공간을 정의했을 때 샘플 간의 거리 관계는 원래의 변수 공간에서의 그것과 차이가 최소화되어야 한다.
4. Nonlinear Feature Extraction(Manifold Learning)
- 다음은 비선형적 결합을 통해 주성분을 생성하는 기법들을 알아보자. 비선형적 결합을 사용하는 차원 축소를 Manifold Learning이라고도 부른다.
4.1. KPCA와 KFDA
- KPCA와 KFDA는 기존 PCA와 LDA에 커널함수를 적용해 비선형적 변수 결합을 만들어내는 방법이다.
- PCA와 LDA는 모두 기존의 변수 공간으로부터 새로운 벡터(선형결합)를 만들고, 이 벡터를 축으로 하는 새로운 변수 공간을 정의하는 것이라고 이해할 수 있다. 그런데 이때 얻어지는 벡터는 결국 직선이기 때문에 변수 공간에서 비선형적으로 분포하는 샘플들에는 부적합하다.
- 따라서 현재의 차원에서 비선형적으로 표현되는 샘플들을 선형적으로 나타낼 수 있는 고차원 공간으로 보낸 후 PCA나 LDA를 사용하는 방법을 떠올릴 수 있다. 이때 계산의 복잡도를 낮추기 위해 커널 함수를 사용한다. 이 방법이 바로 KPCA와 KFDA이다.
4.2. Isomap
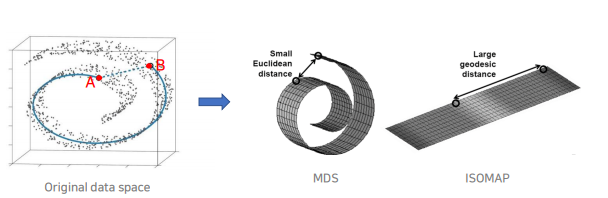
- Isomap은 MDS의 일반화된 버전이라고 할 수 있다. MDS와 유사하게 Isomap은 원래의 변수 공간에서 샘플들 간의 거리 관계가 그대로 유지되도록 하는 새로운 변수 공간을 만들어낸다. 다만 MDS는 샘플이 분포하고 있는 기하학적인 형태를 고려하지 않고 그저 유클리드 거리를 사용해 샘플 간 거리를 계산했다면, Isomap은 샘플이 분포하는 기하학적인 형태를 존중해줄 수 있는 거리 척도를 사용한다는 점에서 다르다.
- 기하학적인 형태를 존중해줄 수 있는 거리 척도란 지오데식 거리를 말한다. 유클리드 거리와 지오데식 거리의 차이점은 아래 그림을 보면 직관적으로 이해할 수 있다. 달팽이처럼 말려있는 형태로 샘플들이 분포하고 있을 때 우리는 두 점 A와 B 간의 거리를 단순히 유클리드 거리로 계산하면 안 될 것 같은 느낌이 든다. 이때 사용할 수 있는 거리 척도가 지오데식 거리이다.
5. 실습
- 저번 포스팅에서 다루었던 신용카드 연체 데이터에 차원 축소를 적용해보자. train set을 분리해 학습시킨 후, 차원 축소 없이 곧바로 로짓 회귀분석, 랜덤 포레스트, 그래디언트 부스트를 적용해보았다.
- 중요한 지점이 있는데, 차원 축소 기법의 대부분은 분산이나 거리 연산을 포함한다. 따라서 차원 축소를 할 때는 스케일의 문제가 매우 치명적일 수 있다. 차원 축소를 할 때는 반드시 스케일링을 동반해야 한다. 여기서는 min-max 스케일링을 사용했다.
- 차원 축소 없이 진행한 결과는 아래와 같다.



- PCA를 진행해보자. 원 데이터는 총 11개의 독립변수를 가지고 있으므로, PCA를 통해 생성된 주성분들도 11개이다. 주성분들의 누적 분산 비율을 계산하면 아래와 같다.
from sklearn.decomposition import PCA
pca=PCA(n_components=11)
X_train_PCA=pca.fit_transform(X_train)
cumulative = []
temp = 0
for i in range(0, 11):
temp += pca.explained_variance_ratio_[i]
cumulative.append(temp)
plt.plot(range(1,12),cumulative)
plt.show()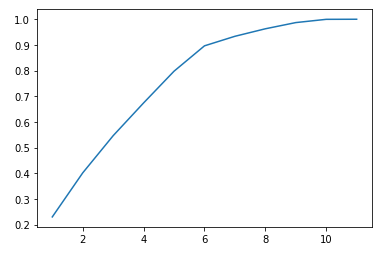
- 만들어진 주성분들 중 분산 비율 상위 7개만 사용해도 전체 분산의 93% 정도를 설명할 수 있다. 즉 11개 변수들을 모두 사용할 필요가 없다. 7개의 주성분만 남기고 다시 로짓 회귀분석과 랜덤포레스트, 그래디언트 부스트를 적용해보았다.
#fit은 주성분을 찾는것, transform은 주성분으로 변환하는 것
pca=PCA(n_components=7)
X_train_PCA=pca.fit_transform(X_train) #train은 fit + transform
X_test_PCA=pca.transform(X_test) #test는 transform. 주성분은 train set에서 찾은 것을 사용해야 함


- 사실 큰 차이는 없었다. PCA로 기대되는 효과는 학습시간은 빨라지면서도 테스트셋에 대한 성능 차이는 적은, 그런 것이다. 다만 주어진 데이터는 원래 칼럼 수가 11개밖에 안 되기 때문에 학습시간이 애초부터 오래 걸리지 않아서 PCA의 효과가 크지 않은 것으로 보인다.
- PCA의 또다른 장점은 차원 수를 획기적으로 줄여 결과의 시각화도 가능하게 한다는 점이다. 분산 비율 상위 2개의 주성분만을 사용하면 클래스의 분포를 시각화할 수 있다. 상위 2개의 주성분을 축으로 하는 평면에서 샘플들의 클래스별 분포도이다.
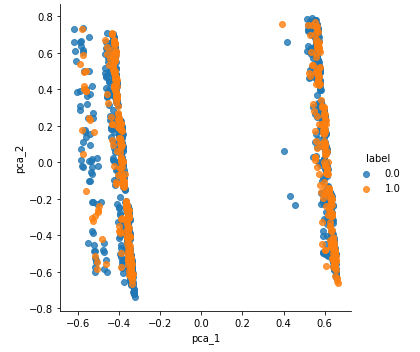
- 큰 효과는 없는 것 같다. 사실 데이터셋의 특징에 따라서 그리고 어떤 차원축소 기법을 적용하느냐에 따라서 결과가 많이 달라질 수 있다.
- PCA의 가장 큰 단점은 '이게 뭐냐?'라는 것이다. 왜냐하면 차원 축소로 생성된 주성분들은 수치적으로 클래스들을 잘 분리한다거나 분산 비율이 최대화된다거나 하는 것일 뿐이다. 따라서 저렇게 그림을 그려놓고 도대체 X축은 뭐고 Y축은 무엇이냐라고 물어도 할 말이 없다. 그냥 분류가 잘 되면 장땡이다, 정도.
'머신러닝&딥러닝' 카테고리의 다른 글
| Deep Learning #1 딥러닝 기초: 심층신경망의 구조와 간단 코드 실습 (0) | 2023.02.15 |
|---|---|
| Machine Learning #5 클러스터링 : 근로자 임금 분포 클러스터링 (0) | 2023.02.12 |
| Machine Learning #3 Decision Tree & Ensemble : 신용카드 연체 예측 (0) | 2023.02.08 |
| Machine Learning #2 Logistic Regression & SVM : 정규직 여부 분류 모델 (0) | 2023.02.07 |
| Machine Learning #1 Linear Regression : 근로자 임금 회귀분석 (0) | 2023.02.06 |