GitHub - SeungbeomDo/Time_Series_Analysis: Practical Codes for Time Series Modeling and Analysis
Practical Codes for Time Series Modeling and Analysis - GitHub - SeungbeomDo/Time_Series_Analysis: Practical Codes for Time Series Modeling and Analysis
github.com
1. 벡터 시계열
1.1. 벡터 시계열의 도입
- 이전 포스팅에서 다루었던 ARMA 모델 등은 단변량 시계열을 분석하는 모델이었다. 가령 주가 시계열 $\{X_{t}\}$은 주식의 가격이라는 하나의 대상을 시간에 걸쳐 관측한 값의 집합이다.
$$\{X_{t}\} = \{X_{1}, X_{2}, ... X_{n}\}$$
- 반면 둘 이상의 시계열을 동시에 관측할 수도 있다. 가령 주가 시계열 $\{X_{t}\}$과 채권 수익률의 시계열 $\{Y_{t}\}$을 함께 관측해서 나타낼 수도 있다. 이는 주어진 시점 t에서의 주가와 채권 수익률을 원소로 하는 2차원 벡터의 시계열이 된다.
$$ \begin{bmatrix} X_{t} \\ Y_{t} \end{bmatrix} =\{ \begin{bmatrix} X_{1} \\ Y_{1} \end{bmatrix}, \begin{bmatrix} X_{2} \\ Y_{2} \end{bmatrix}, ... , \begin{bmatrix} X_{n} \\ Y_{n} \end{bmatrix} \}$$
- 이렇게 시계열의 원소가 스칼라가 아닌 벡터일 때, 주어진 시계열을 벡터 시계열이라고 한다. 편의상 임의의 벡터 시계열을 $\vec{Z_{t}}$로 나타내자.
1.2. 벡터 시계열의 정상성
- 벡터 시계열도 시계열의 한 형태이기 때문에, 시계열의 정상성 논의에서 예외가 아니다. 스칼라 시계열의 정상성 정의를 자연스럽게 벡터로 확장하면 된다. 주어진 m차 벡터 시계열 $\vec{Z_{t}}$가 다음의 성질들을 만족하면 정상적 벡터 시계열이다.
$$E[\vec{Z_{t}}] = \vec{\mu} = \begin{bmatrix} \mu_{1} \\ \mu_{2} \\ \vdots \\ \mu_{m} \end{bmatrix}$$
$$Cov[\vec{Z_{t}}; k] = E[(\vec{Z_{t}}-\vec{\mu})(\vec{Z_{t-k}}-\vec{\mu})'] = \begin{bmatrix} \gamma_{11}(k) ... \gamma_{1m}(k) \\ \vdots \\\gamma_{1m}(k) ...\gamma_{mm}(k) \end{bmatrix}$$
- 즉, 벡터시계열의 평균은 시간에 대하여 상수이고 자기공분산 행렬은 시차(time lag; k)에 대해서는 함수이지만 시간에 대해서는 상수이다.
2. VAR 모형
2.1. VAR(1) 모형
- VAR(Vector AutoRegressive) 모형이란 벡터 시계열에 대한 AR process를 말한다. 당연히 벡터 시계열의 ARMA process도 가능하지만 실제 문헌에서는 보통 AR process만을 사용한다.
- 가장 간단한 VAR 모형인 2차원 VAR(1) 모형은 다음과 같이 정의된다.
$$\begin{bmatrix} Z_{1t} \\ Z_{2t} \end{bmatrix} = \begin{bmatrix} \phi_{11} \phi_{12} \\ \phi_{21} \phi_{22} \end{bmatrix} \begin{bmatrix} Z_{1,t-1} \\ Z_{2,t-1} \end{bmatrix} + \begin{bmatrix} \epsilon_{1t} \\ \epsilon_{2t} \end{bmatrix}$$
- 여기서 $t-1$ 시점 벡터의 계수는 계수 행렬이라고 하며, 오차 벡터는 평균이 0이고 공분산이 $\sigma_{12}$인 2변량 정규분포를 따른다고 가정한다. 위 식을 풀어서 쓰면 아래와 같다.
$Z_{1t} = \phi_{11}Z_{1,t-1} + \phi_{12}Z_{2,t-1} + \epsilon_{1t}$
$Z_{2t} = \phi_{21}Z_{1,t-1} + \phi_{22}Z_{2,t-1} + \epsilon_{2t}$
이때, $\epsilon_{1t} \sim N(0, \sigma_{1}^{2})$, $\epsilon_{2t} \sim N(0, \sigma_{2}^{2})$, and $Cov(\epsilon_{1t}, \epsilon_{2t}) = \sigma_{12}$
- 흥미로운 것은 각 시계열은 자신의 이전 기 값에도 영향을 받지만, 다른 시계열의 이전 값에도 영향을 받는다는 것이다. 가령 주가와 금리로 구성된 2차 벡터시계열을 본다면 오늘의 주가는 어제의 주가에 영향도 받지만 어제의 금리에도 영향을 받는 모형이 된다. 단변량 시계열 모형보다 훨씬 현실성이 높아졌다는 것을 알 수 있다.
2.2. VAR(p) 모형과 정상성 조건
- 앞서 다룬 단순한 모형을 조금 더 일반화하자. m차원 벡터 시계열에 대한 AR(p) 모형은 다음과 같이 정의된다.
$$\vec{Z_{t}} = \vec{c} + \Phi_{1}\vec{Z_{t-1}} + \Phi_{2}\vec{Z_{t-2}} + ... + \Phi_{p}\vec{Z_{t-p}} + \vec{\epsilon_{t}}$$
- 상수항 벡터 $\vec{c}$와 각각의 시차항에 대응하는 $m*m$ 계수 행렬을 포함하고 있다.
- 벡터 시계열에 대해서도 AR polynomial을 사용해 간편하게 나타낼 수 있다.
$$\Phi(L)\vec{Z_{t}} = \vec{c} + \vec{\epsilon_{t}}$$
이때, $\Phi(L) = I - \Phi_{1}L - ... - \Phi_{p}L^{p}$, $I$는 항등행렬
- VAR(p) process의 정상성 조건은 $\Phi(L) = 0$의 모든 p개의 근 $L$의 결정계수(determinant)가 1보다 커야 한다는 것이다.
3. VAR 모형의 식별과 추정
- 소비자물가지수 상승률(전월 대비)에 금리상승률(전월대비, 말일기준)이 미치는 영향을 VAR 모형으로 알아보자.
- 이때 단순히 소비자물가지수 상승률을 금리상승률에 회귀시키는 모형을 생각할 수도 있지만
- 소비자물가지수와 금리 간의 영향력은 상호적이다. 금리가 올라서 물가가 내릴수도 있지만, 물가가 올라서(수요가 늘어나서) 금리가 오르는 것도 가능하다.
- 또한 경제변수 간에는 시차를 둔 인과관계가 존재하는 경우가 많다. 금리가 올랐을 때 즉각적으로 물가가 낮아진다기보다는 몇 개월 정도 시차를 두고 효과가 나타난다고 보는 것이 자연스럽다.
- 따라서 소비자물가지수와 금리 간의 상호 인과관계와 시차를 둔 인과관계를 모형에 반영해주기 위해서는 VAR 모형이 더 적합하다.
3.1. VAR 모형의 식별
- VAR 모형의 파라미터 p를 결정해주기 위해서는 AIC를 사용한다. 물론 단변량 시계열에서처럼 ACF/PACF를 구하는 방법도 있지만, 벡터 시계열의 경우 서로 다른 시계열 간의 상관관계가 개입하므로 간단한 문제가 아니다. 실용적으로는 AIC를 최소화하는 모델 파라미터를 찾으면 된다. 물론 그 외에도 BIC, HQ, LR 등의 통계량도 자주 사용한다.
- 소비자물가지수 상승률과 콜금리 상승률의 VAR 모형을 식별하기 위해 AIC를 기준으로 최적의 시차를 선택하였다. AIC를 기준으로 시차가 4(개월)일 때가 가장 적합한 모형이라는 결과를 얻었다.
from statsmodels.tsa.api import VAR
forecasting_model = VAR(data.iloc[:, [1,6]])
results_aic = []
for p in range(1,24):
results = forecasting_model.fit(p)
results_aic.append(results.aic)
plt.plot(range(1,24), results_aic)
plt.show()
print('minimum AIC is {0}, with time lag of {1}'.format(np.min(results_aic), np.argmin(results_aic)+1))
x축은 시차, y축은 AIC이다. AIC가 가장 낮은 시차가 VAR 모형의 p가 된다.
3.2. VAR 모형의 추정
- 시차 4 하에서 식별된 VAR(4) 모형은 총 2 * 시차 4 * 벡터 차원 2 = 16개의 독립변수 계수와 오차항 2개의 공분산, 총 18개의 모수를 가지는 모델이 된다. 모수는 OLS로 추정할 수 있다.
- 추정된 모형으로부터, 시차를 둔 콜금리가 소비자물가지수와 콜금리에 미치는 영향력은 아래와 같다. y축은 베타값이고 x축은 시차이다.

- 또한 시차를 둔 소비자물가지수가 콜금리와 소비자물가지수에 미치는 영향력은 아래와 같다.
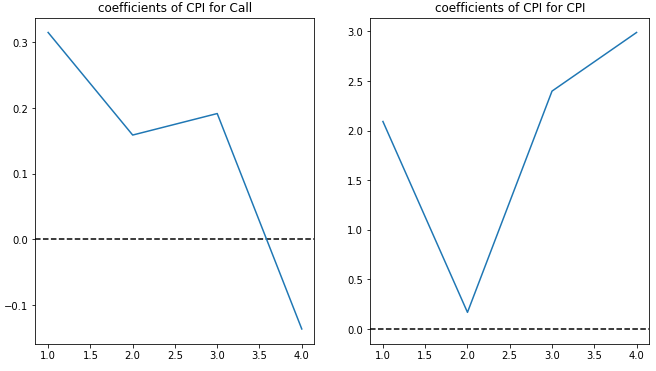
- 콜금리는 2~3개월의 시차를 두고 소비자물가지수에 음의 영향력을, 소비자물가지수는 1~3개월의 시차를 두고 콜금리에 양의 영향력을 미치는 것으로 나타났다.
3.3. 모형의 검정
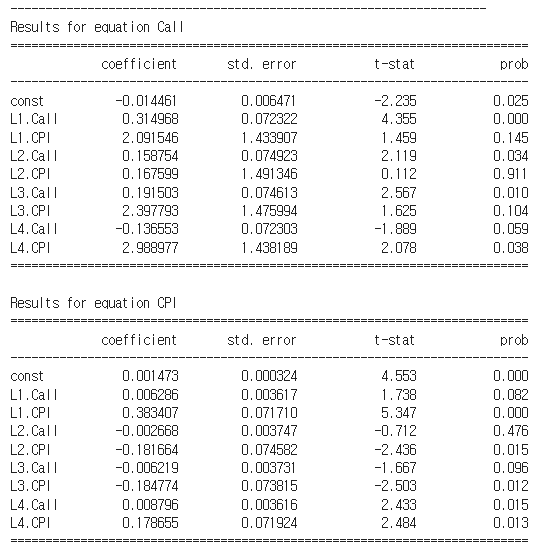
- 단변량 시계열의 ARIMA 모형에서 그러했듯이, VAR 모형도 회귀계수와 잔차에 대한 검정을 실시한다. 언급한 모형의 베타계수들에 대한 검정결과는 아래와 같다. 몇가지 베타값은 유의수준 0.1 하에서 귀무가설을 기각하지 못했음을 알 수 있다. 가령, 콜금리에 대한 시차 2의 소비자물가지수 등이다.
- 다음은 잔차검정이다. 모델이 유효한 예측을 제시한다면, 모형의 잔차 시계열은 독립이어야 한다. 자주 사용하는 검정은 포트맨토 검정으로, 주어진 잔차 시계열의 자기상관계수가 0이라는 것이 귀무가설이다. 검정 결과 귀무가설을 기각하지 못해 모형이 유효하다는 것을 보였다.
forecast_model_fit.test_whiteness(10, 0.05, False).summary()
- 샘플 내에서의 적합된 값은 아래와 같다. test set에 대한 결과는 아니므로 정확한 성능은 아니다.

'시계열&계량경제학' 카테고리의 다른 글
| DeepAR (0) | 2023.02.24 |
|---|---|
| 시계열 분석 #11: VAR 모형의 이슈들 (0) | 2023.02.15 |
| 시계열 분석 #9 ARCH & GARCH (0) | 2023.02.11 |
| 시계열 분석 #8 Auto ARIMA & Backtesting (2) | 2023.02.08 |
| 시계열 분석 #7 Box-Jenkins-Method (0) | 2023.02.03 |