시계열 예측 모델링에 사용하는 Box-Jenkins-Method를 설명한다. 특별한 방법론이라기보다는, 전통적인 시계열 모델을 구현하는 데 있어서 사용하는 매뉴얼이라고 이해할 수 있다. 총 5가지 단계로 이루어지는데,
- 주어진 시계열의 정상성 여부를 테스트한다. 비정상 시계열일 경우 차분, 필터링 등 적당한 처리를 거쳐 정상화한다.
- ARMA 모델의 모수인 p와 q를 정한다.
- 모델의 계수들을 추정한다.
- 적합한 모델인지 알아보기 위해 계수 검정 및 잔차 검정을 실행한다.
- 최종 모델을 사용하여 예측한다. 이때 차분된 시계열을 역차분하여 원 시계열로 돌려준다.
그럼 한 단계씩 살펴보도록 하자.
1. 정상성 검정과 정상화
1.1. 정상성의 의의
- 첫 단계는 주어진 시계열의 정상성 여부를 파악하는 것이다. 간단한 방법으로는 시계열을 시각화하여 추세나 계절성을 눈으로 확인하는 것이다. 가령 아래는 삼성전자 주가의 시계열이다.
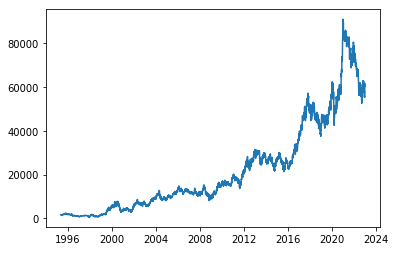
- 삼성전자 주가는 증가하는 추세를 가지고 있어, 시간에 대하여 평균과 분산이 증가할 것임을 짐작할 수 있다. 즉 비정상 시계열이다.
- 정상성은 왜 문제가 되는가? 우리가 예측 모델을 구현하기 위해서는 주어진 샘플을 통해 모집단의 정보를 추정해야 한다. 가령 내일의 삼성전자 주가를 예측하고자 한다면 삼성전자가 상장된 시점부터 오늘까지의 삼성전자 주가 샘플을 사용해 모수를 추정해야 한다.
- 그런데 위의 샘플로부터 주가의 평균을 추정하면? 대략 2만원~3만원 정도가 나올 것이다. 그런데 내일 삼성전자 주가가 평균적으로 2~3만원이라는 추정은 비현실적이다.
- 삼성전자 주가의 평균이 시간에 대해 증가하는 성질이 있음에도 이를 고려하지 않고 샘플로부터 무작정 표본 평균을 구하면 된다는 오류를 범하는 것이다.
- 만약 삼성전자 주가의 평균이 시간에 대해 일정하다면(정상 시계열이라면) 표본에서 구한 평균이 내일의 주가 평균을 구하는 데 유의미한 정보로 활용될 수 있을 것이다. 하지만 지금은 그렇지 않다.
1.2. 정상성의 검정
- 이전 포스팅에서 밝혔듯 정상성의 대표적인 검정 방법은 ADF 검정과 KPSS 검정이 있다. 두 가지 검정을 모두 수행하여 주어진 시계열의 정상성 여부를 살핀다.
- ADF test를 실시한 결과 "귀무가설: 주어진 시계열은 단위근이 존재한다(비정상 시계열이다)"를 기각할 수 없었다.

- KPSS test를 실시한 결과 "귀무가설: 주어진 시계열은 trend-stationary하다"를 기각했다.
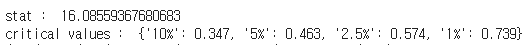
- 두 검정의 결과가 일치된 방향으로 나타나므로 주어진 주가 시계열은 비정상 시계열이다.
1.3. 차분
- 주어진 시계열이 정상 시계열이 아니라는 결과를 얻었기 때문에, 차분을 통해 정상 시계열로 바꿔준다. 이때 꼭 차분을 해야 하는 것은 아니고 필터링이나 요소분해 방법을 통해 추세를 제거하는 것도 좋은 대안이 될 수 있다.
- 주가 시계열의 경우 로그 차분을 통해 수익률을 구하는 것이 정상 시계열로 변환하는 일반적인 테크닉이다.
- 시계열 $X_{t}$에 대하여 연산 $Log\frac{X_{t}}{X_{t-1}}$을 로그차분이라고 한다. 이 값은 사실 주가의 수익률과 수치적으로 거의 근사하다. 로그차분된 시계열을 수익률 시계열이라고 해도 무방하다.
- 로그차분의 결과 수익률 시계열은 다음과 같다. 정상성을 기대해도 좋을 것 같은 패턴이 드러난다.
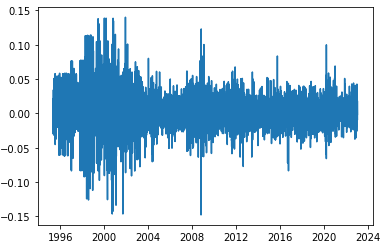
- ADF 검정을 실시한 결과, 귀무가설을 기각했다.

- KPSS 검정의 결과, 귀무가설을 기각하지 못했다.
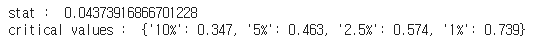
- 따라서 수익률 시계열은 정상 시계열이라고 할 수 있다.
2. 모델 파라미터 결정
- 정상 시계열을 ARMA 모형으로 적합할 때, ARMA 모형의 모수 p, q를 정해주어야 한다.
- 이전 포스팅에서 다루었듯이 정상적이고 가역적인 ARMA(p, q) 시계열의 ACF는 시차 q에서, PACF는 시차 p에서 빠르게 값이 감소하는 형태를 보인다. 이 사실을 활용하여 p와 q를 정할 수 있다.
- 수익률 시계열의 ACF와 PACF는 아래와 같다.
from statsmodels.tsa.stattools import acf, pacf
plt.figure(figsize = (16,8))
plt.subplot(1,2,1)
lag_acf = acf(data['Return'], nlags=20)
plt.plot(np.arange(21), lag_acf)
plt.xticks(np.arange(21))
plt.ylim(-0.2, 1.2)
plt.axhline(0, color = 'black', linestyle = '--')
plt.axhline(y=-1.96/np.sqrt(len(data['Return'])),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(data['Return'])),linestyle='--',color='gray')
plt.title('Auto Correlation')
plt.xlabel('Time Lag')
plt.ylabel('Auto Correlation')
plt.subplot(1,2,2)
lag_pacf = pacf(data['Return'], nlags=20, method='ols')
plt.plot(np.arange(21), lag_pacf)
plt.xticks(np.arange(21))
plt.ylim(-0.2, 1.2)
plt.axhline(0, color = 'black', linestyle = '--')
plt.axhline(y=-1.96/np.sqrt(len(data['Return'])),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(data['Return'])),linestyle='--',color='gray')
plt.title('Partial Auto Correlation')
plt.xlabel('Time Lag')
plt.show()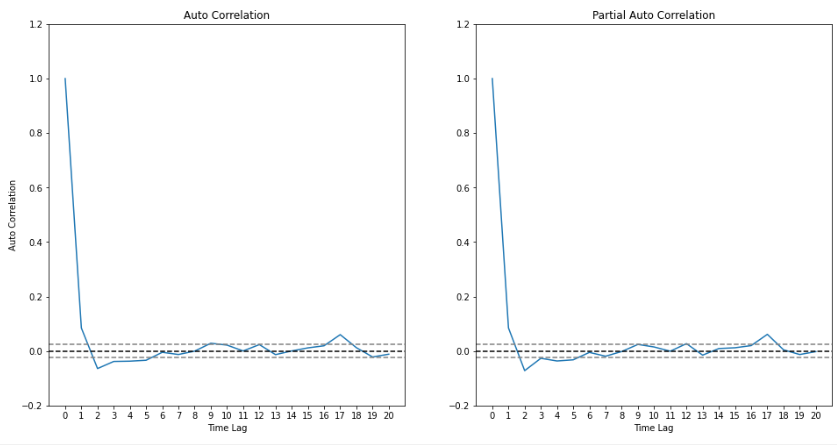
- 회색 점선은 상관계수가 제로라는 귀무가설 하의 95% 신뢰구간이다. 즉 이 구간을 넘어서는 상관계수들만 통계적으로 유의하다고 할 수 있다. 귀무가설이 참일 때 ACF와 PACF는 $N(0, \frac{1}{n})$을 따른다고 알려져있다. $n$은 샘플의 크기이다.
- 그래프의 형태로 보아 p=2, q=1 정도면 적합한 모델일 것으로 생각할 수 있다.
3. 모델 추정
- ARMA(p,q) 모델의 p, q를 확정하였다면 설계된 회귀식의 계수들을 추정하는 일이 남았다. 이는 다음 회귀식에서 $\phi_{1}$, $\phi_{2}$, 그리고 $\theta_{1}$를 추정하는 일이다.
$$X_{t} = \phi_{1} X_{t-1} + \phi_{2} X_{t-2} + \theta_{1} \epsilon_{t-1} + \epsilon_{t}$$
- ARMA 모델 중 AR 요소의 계수를 추정할 때는 최우추정법(Maximum Likelihood Estiamtion; MLE)을 사용한다. ARMA model의 MLE는 IID 가정 하의 MLE와 조금 다른 면이 있는데 차후 포스팅에서 다루어보도록 하자.
- ARMA model의 구현은 아래와 같다. statsmodels 패키지의 ARIMA 라이브러리를 사용하는 데, 주요한 옵션은 모델 파라미터와 방정식 형태이다.
from statsmodels.tsa.arima_model import ARIMA
model = ARIMA(data['Return'], order=(2,0,1))
model_fit = model.fit(trend = 'nc')
model_fit.summary()- order 옵션은 ARIMA의 파라미터 (p,d,q)를 의미한다. 수익률 시계열은 이미 정상시계열이므로 d=0이다.
- trend 옵션은 회귀식이 절편이나 선형추세를 포함하는지 여부이다. 수익률 시계열은 평균이 0이고 특별한 추세가 존재하지 않는다는 가정 하에 절편항과 선형추세항를 모두 배제하고 추정한다.
- 결과는 아래와 같다. 모형의 추정계수가 모두 통계적으로 유의하고, 로그우도값이나 AIC, BIC를 기준으로 할 때도 적절해보인다. 로그우도는 높을수록, AIC와 BIC는 낮을수록 좋다. AIC와 BIC는 시계열 모형을 평가하는 주요한 지표인데 이것도 다음 포스팅으로 미루겠다..
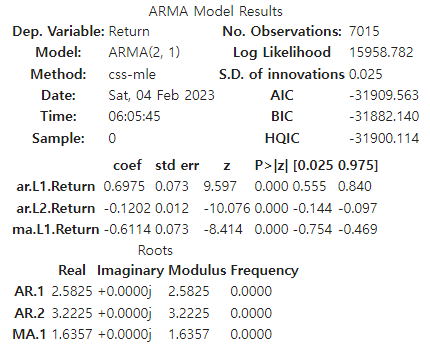
4. 모델 검증
- 구현된 모델의 예측값과 실제 데이터를 비교해보자. 우선 여기서 다루는 내용은 train set과 test set을 분리하지 않았음에 유의하자.
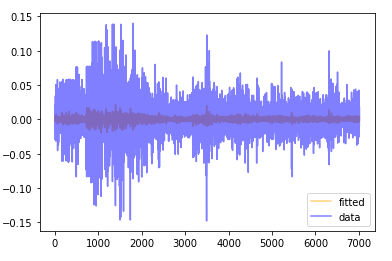
- 파란 선은 실제 수익률이고, 음영으로 나타난 주황색 선은 모델의 예측값이다. 차이가 크다고 할 수도 있지만 모델의 추정이라는 것이 조건부 평균을 추정하는 것이라는 점을 상기하자. 데이터와 예측값의 차이는 랜덤하게 발생하는 잔차가 된다.
- 보다 엄밀한 검증은 잔차검정으로 이루어진다. 만약 우리의 ARMA 모델이 수익률 시계열을 잘 적합했다면, 모델로 설명되지 않는 잔차들은 랜덤 시계열이어야 할 것이다. 잔차 시계열은 아래와 같다.
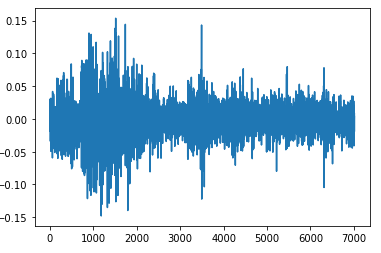
- Ljung-Box 검정으로 잔차 시계열의 자기상관이 시차들에 대하여 모두 0인지 검정해보았다.
import statsmodels.api as sm
def LJ_result(ts):
result = []
for lag in np.arange(1, 11, 1):
result.append(sm.stats.acorr_ljungbox(ts, lags=[lag])[1][0])
return pd.DataFrame({'lag':np.arange(1,11,1), 'p_value':result})
LJ_result(data['Return_Error']).T
- 시차를 10까지 두고 검정해본 결과, 자기상관계수가 모두 0이라는 귀무가설을 모두 기각하지 못했다. 즉 모델의 잔차시계열이 white noise라고 할 수 있다(독립이라는 뜻은 아님).
- 원 수익률 시계열에 대해서도 비슷한 결과가 나오는 것이 아닐까 하여 같은 검정을 해보았는데 모든 시차에 대하여 귀무가설을 기각했다. 즉 원 수익률 시계열은 자기상관이 존재하는 시계열이었다. 모델 적합을 통해서 자기상관이 존재하는 부분은 예측해내고, 예측할 수 없는 부분만 잔차로 남았다는 것이 확인된 셈이다.

5. 예측과 역차분
- 지금까지는 수익률 시계열을 가지고 진행한 것이었는데 사실 우리는 주가 시계열을 예측하는 것이 목표이다.
- 예측된 수익률 시계열을 주가 시계열로 바꾸기 위해서는, 수익률과 주가 간의 다음과 같은 관계식을 활용하면 그만이다.
$$P_{t} = P_{t-1} * (1 + R_{t})$$
where $P_{t}$ : t 시점 주가, $R_{t}$ : t 시점 수익률
- 어차피 주가를 예측할 때는 내일 주가가 문제인 것이고 우리는 오늘 주가까지는 다 알고 있다. 따라서 오늘 주가에 예측된 내일의 수익률 시계열을 곱해서 내일 주가의 예측으로 사용하면 된다.
- 아래에서 Close_shift 칼럼은 t-1 시점 주가, Fitted_Return은 t 시점의 예측된 수익률을 의미하므로 둘을 곱하면 t 시점의 예측된 주가인 Fitted_Close 칼럼을 얻는다.
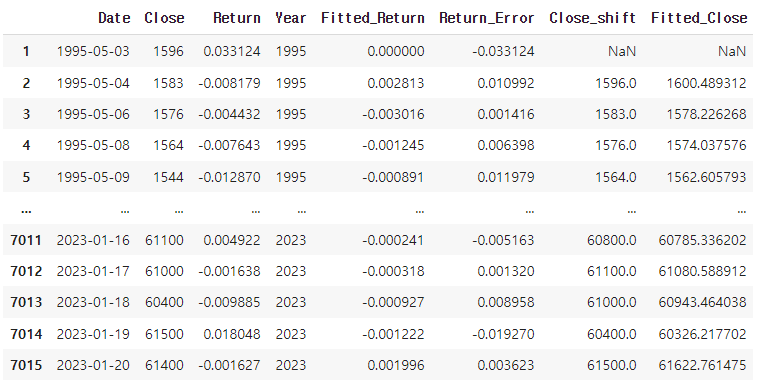
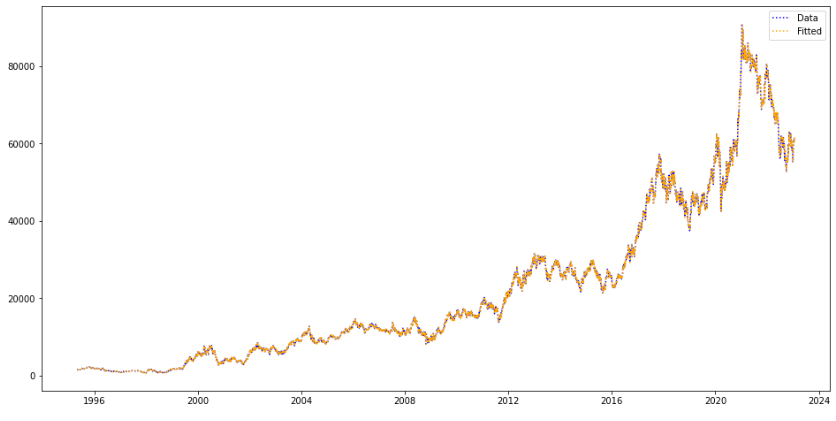
- 큰 스케일에서 보면 예측된 값과 실제값이 겹쳐서 차이가 드러나지 않는다. 2022년 동안의 그것으로 좁혀서 보면
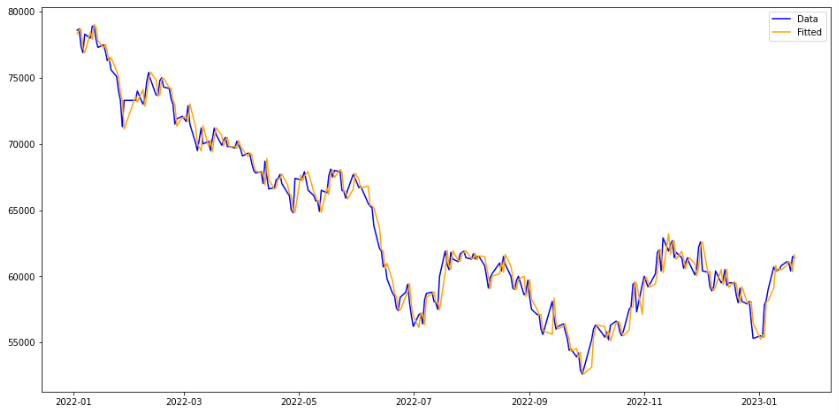
- 대충 잘 맞는 것 같기도 한데, 오차는 꽤 크다. RMSE는 485가 나오는데 주가 시계열의 스케일이 시간에 대해 증가하면서 오차도 시간에 대해서 분산이 증가하는 경향이 있다. 따라서 RMSE는 믿을만한 지표가 아니다.
- 주가를 예측하는 시점이 바로 직전 거래일이라고 하면, 사용한 정보 대비 오차를 알아보기 위하여, 오차제곱을 직전 거래일 주가로 나눈 값의 평균을 구했다.
$$\sqrt{\Sigma_{t=1}^{T} [\frac{예측종가_{t} - 실제종가_{t}}{실제종가_{t-1}}] ^{2}}$$
- 그 제곱근을 구해 원 데이터와 단위를 맞춰주면 0.025 정도가 나온다. 오늘 주가가 6만원이라면 모델을 가지고 예측한 내일 주가의 오차가 6만 * 2.5% = 1500원 정도된다는 뜻이다. 별로 안 좋은 모델 같다.
- 그리고 이건 사실 test set을 분리하지 않고 진행한 결과이다. 정확한 성능을 보려면 train set에 대해서만 적합해서 test set을 한 번에 맞추어야 한다. 좀더 정확하게 보려면 백테스팅을 해야하는데, 학습한 모델에 오늘까지의 주가를 적용하여 내일 주가를 예측하고, 내일 시점에서는 내일까지 주어진 주가 정보를 적용하여 내일 모레 주가를 예측하고, ... 하는 식으로 성능을 측정해봐야 한다. 왜냐면 이게 실제 트레이더들이 매일매일 주가를 예측하는 과정과 흡사하기 때문이다.
'시계열&계량경제학' 카테고리의 다른 글
| 시계열 분석 #9 ARCH & GARCH (0) | 2023.02.11 |
|---|---|
| 시계열 분석 #8 Auto ARIMA & Backtesting (2) | 2023.02.08 |
| 시계열 분석 #6 정상성 검정 (1) | 2023.02.03 |
| 시계열 분석 #5 MA process와 ARMA process (0) | 2023.02.03 |
| 시계열 분석 #4 white noise와 AR process (0) | 2023.02.02 |