GitHub - SeungbeomDo/Time_Series_Analysis: Practical Codes for Time Series Modeling and Analysis
Practical Codes for Time Series Modeling and Analysis - GitHub - SeungbeomDo/Time_Series_Analysis: Practical Codes for Time Series Modeling and Analysis
github.com
1. 변동성의 자기상관
- 시계열 모형에서 오차항은 말그대로 오차, 즉 예측불가능한 시계열 요소로 간주된다. 그러나 오차항 자체가 아닌 오차항의 '분산'은 예측할 수 있다는 것이 많은 시계열 데이터에서 관찰되는 사실이다.
- 특히 금융 시계열에서 그러한데, 가령 주식시장에 어떤 충격이 발생하면 높은 변동성이 한동안 사라지지 않고 지속된다. 아래는 KOSPI 지수의 수익률 시계열인데, 수익률 자체는 예측하기 어려운 시계열로 보이지만, 수익률의 분산은 그 값이 높은 시기와 그렇지 않은 시기가 뚜렷하게 구분된다. 이처럼 높은 변동성이 시간적으로 집중되는 현상을 변동성의 군집현상(Clustering)이라고 부르기도 한다. 그래서 수익률 자체는 예측하기 어려워도 수익률의 분산은 예측할 수 있지 않을까 하는 아이디어가 제시되었다.
- 그런데 처음에는 오차의 분산을 예측한다고 말했다가 이제는 수익률의 분산을 예측한다고 하면서 말이 왔다갔다하는 것이 다소 혼란스러울 수도 있다. 이전 포스팅들에서도 살펴본 사실이지만 수익률은 오차항의 비중이 매우 크다. 따라서 수익률에 대해 논의하는 것은 오차에 대해 논의하는 것과 거의 같다는 점을 상기하면 혼란이 덜하지 않을까 싶다.
2. ARCH 모형 (AutoRegressive Conditional Heteroskedasticity)
2.1. ARCH 모형의 도입
- 다음과 같은 간단한 AR(1) process를 생각해보자.
$$X_{t} = c + \phi X_{t-1} + u_{t}$$
- 여기서 오차항 $u_{t}$는 다음과 같은 white noise process로 가정되는 것이 일반적이다.
$E[u_{t}] = 0$, $Var[u_{t}] = \sigma_{u}^{2}$
- 그런데 위의 정의는 무조건부 분산(unconditional variance)이다. 우리는 시장에서 어떤 충격이 발생했는지 여부에 따라 분산이 변화할 수 있다는 가정을 도입하고자 한다. 이런 아이디어는 다음과 같은 조건부 분산의 정의로 이어진다.
$$\sigma_{t}^{2} = Var[u_{t}|u_{t-1}, u_{t-2}, ...]$$
- 과거에 주어진 시장의 충격에 대한 정보를 오차항 $u_{t-1}, u_{t-2}, ...$ 의 집합으로 나타낸다면 위와 같은 모델이 된다. 이렇게 정의된 조건부 분산은 과거에 주어진 오차항의 값에 따라 달라질 수 있다는 점이 반영돼있다. 즉,
$$\sigma_{t}^{2} = \alpha_{0} + \alpha_{1} u_{t-1}^{2} + \alpha_{2} u_{t-2}^{2} + ... + \alpha_{q} u_{t-q}^{2}$$
- 잠깐 멈추고 생각해보자. 조건부 분산이 현재까지 주어진 정보에 따라 다른 값을 갖는다는 것은, 무조건부 분산이 상수라는 정상성의 가정과 상충되지 않을까? 당연히 답은 '그렇지 않다'이다.
- 정상성의 가정은 무조건부 분산이 상수라는 뜻이다. 내일의 분산이나 내일 모레의 분산이나 아무런 조건이 없을 때는 같다는 뜻이다.
- 반면 ARCH 모형에서 얘기하는 '조건부 분산이 달라질 수 있다'란, 오늘 어떤 사건이 발생했느냐에 따라 내일 분산이 달라진다는 뜻이다. 이것은 Identity(정상성)보다는 Independence(독립성)에 관한 이야기이다.
- AR process로 주가를 설명할 때, 오늘의 주가가 어제의 주가에 영향을 받는다고 설명한다(dependence). 하지만 그렇다고 오늘의 주가와 어제의 주가가 동일한 확률분포를 가진다는 가정(identity)에는 영향을 주지 않았다. 분산에 대해서도 그렇게 이해하면 된다.
- 다시 돌아와서, 위에 적은 식에는 사실 다음과 같은 식이 숨어있다.
$\sigma_{t}^{2} = Var[u_{t}|u_{t-1}, u_{t-2}, ...] = E[u_{t}^{2}|u_{t-1}, u_{t-2}, ...]$이므로
$$u_{t}^{2} = \alpha_{0} + \alpha_{1} u_{t-1}^{2}+ \alpha_{2} u_{t-2}^{2} + ...+ \alpha_{q} u_{t-q}^{2} + w_{t}$$
이때, $w_{t} \sim w.n.(0, \lambda^{2})$
- 갑자기 이런 식을 들이밀어서 혼란이 있을 수도 있지만, 설명하는 사람마다 접근법이 다르기 때문에, 오히려 혼란을 방지하기 위하여 다른 데 가서 봤을 만한 이야기를 적은 것뿐이다.
- 이제 ARCH(q) 모형을 깔끔하게 정의하자. ARCH(q) 모형은 시계열 그 자체의 모형인 AR(p) 모형과 AR(p) 모형의 오차 분산을 모형화한 ARCH(q) 모형의 두 가지로 함께 정의된다. 왜냐하면 모형의 오차 분산을 이야기하려면 원래 모형이 뭐였는지도 함께 이야기해줘야 하기 때문이다.
- AR(1)-ARCH(q) 모형은 다음과 같다.
$$X_{t} = c + \phi X_{t-1} + u_{t}$$
$$\sigma_{t}^{2} = \alpha_{0} + \alpha_{1} u_{t-1}^{2} + \alpha_{2} u_{t-2}^{2} + ... + \alpha_{q} u_{t-q}^{2}$$
- 첫번째 식은 AR(1) process이고 평균방정식(mean equation)이라고도 부른다. 두번째 식은 ARCH(q) 모형이며 분산방정식(variance equation)이라고 부른다.
- 어떤 주가수익률을 이런 식으로 모델링한다면, (1) 주가수익률의 시계열은 AR(1) process를 따르고, (2) 이때 모형의 잔차의 분산은 과거 잔차의 제곱항들에 따라 변화한다는 뜻이다. 잔차 제곱항을 시장에 발생한 충격이라고 생각하면 ARCH 모형의 의의가 더 와닿을 듯하다.
2.2. ARCH 모형의 정상성 조건
- ARCH(q) 모형의 평균방정식은 AR process이다. 그리고 이 AR process는 정상적이어야 한다. ARCH(q) 모형이 분산이 시간에 따라 변화하는 것을 모형화했다면서 왜 정상성을 언급하는지 헷갈릴 수 있다. 분명히 구분해야 할 것은, ARCH 모형이 모형화한 것은 조건부 분산(conditional variance)이고, 시계열의 process가 정상적이라고 할 때는 무조건부 분산이 상수인 것을 의미한다는 점이다.
- AR(1) process의 무조건부 분산은 다음과 같이 구한다.
$$\sigma_{u}^{2} = Var[u_{t}] = E[u_{t}^{2}] = E[\alpha_{0} + \alpha_{1} u_{t-1}^{2}+ \alpha_{2} u_{t-2}^{2} + ...+ \alpha_{q} u_{t-q}^{2} + w_{t}] $$
$$= \alpha_{0} + (\alpha_{1} + \alpha_{2} + ...+ \alpha_{q})E[u_{t}^{2}] = \alpha_{0} + (\alpha_{1} + \alpha_{2} + ...+ \alpha_{q})Var[u_{t}]$$
$$\therefore Var[u_{t}] = \frac{\alpha_{0}}{1-\alpha_{1}-\alpha_{2}-...-\alpha_{q}}$$
- AR(1) process이 정상적이려면 무조건부 분산은 유한한 값을 가져야 한다. 따라서 ARCH(q) 모형의 정상성 조건은
$$\alpha_{1}+\alpha_{2}+...+\alpha_{q}<1$$
- 그리고 ARCH 분산 방정식은 다음의 두 가지 조건을 추가적으로 만족해야 한다. 현실의 변동성을 묘사하기 위해서는 당연한 조건이지만, 수리적으로는 이 조건이 만족되지 못하는 경우가 있기 때문에 추가되는 조건이다.
$u_{t}^{2} > 0$ and $\sigma_{t}^{2} > 0$
2.3. ARCH 모형과 Fat-Tailness
- ARCH 모형의 아주, 아주 매력적인 지점은 오차의 조건부 분산이 오차제곱항의 회귀식으로 나타날 때, 주식시장 수익률의 Heavy-Tailed 분포까지 설명된다는 점이다. Heavy-Tailed 분포란 꼬리가 두꺼운 분포, 즉 극단적인 사건이 발생할 확률이 큰 분포를 의미한다. 다른 말로 Fat-Tailness라고도 표현한다.
- 아래 그림은 KOSPI 일별 수익률의 qq plot이다. X축은 표준정규분포의 분위수이고 Y축은 일별 수익률의 분위수이다. 45도 직선은 표준정규분포의 qq plot을 나타내는데, 실제 qq plot은 직선의 좌측 극단에서는 직선을 하회하고 우측 극단에서는 직선을 상회한다. 그리고 그 정도도 매우 크다.
- 이는 표준정규분포를 따른다면 이렇게까지 낮거나 높은 수익률이 자주 나타나서는 안 된다는 뜻, 다시 말해 수익률 분포가 매우 두꺼운 꼬리를 가지고 있다는 뜻이다.
- ARCH 모형은 이런 두꺼운 꼬리 분포가 반영돼있다. 어떻게 그러한지 수리적으로 확인해보자. 먼저 다음과 같은 $\nu_{t}$를 정의하자. $\nu_{t}$를 사용하면 오차항 $u_{t}$를 다음과 같이 쓸 수 있다.
$$\nu_{t} = \frac{u_{t}}{\sigma_{t}}$$
$$u_{t} = \sigma_{t}\nu_{t}$$
- 이때 $\nu_{t} \sim N(0,1)$이라고 가정하더라도 $u_{t}$의 정의와는 아무런 모순이 없다. 한편 오차의 조건부 분산은 다음과 같은 ARCH(1) process를 따른다.
$$\sigma_{t}^{2} = \alpha_{0} + \alpha_{1} u_{t-1}^{2}$$
- 이제 $u_{t}$의 첨도(kurtosis)를 구해보자.
$$E[u_{t}^{4}] = E[E[u_{t}^{4}|u_{t-1}, ... ]] = E[E[\sigma_{t}^{4}\nu_{t}^{4}|u_{t-1}, ... ]] = E[\nu^{4}_{t}]E[(\sigma_{t}^{2})^{2}|u_{t-1}, ... ]$$
- $\nu$가 정규분포를 따르면 $E[\nu^{4}] = 3$이고, $\sigma_{t}^{2}$의 분산 방정식으로부터
$$E[u_{t}^{4}] = 3(\alpha_{0}^{2} + 2\alpha_{0}\alpha_{1}E[u_{t-1}^{2}]+\alpha_{1}^{2}E[u_{t-1}^{2}])$$
- 주어진 시계열이 정상시계열이라면 무조건부 분산 $E[u_{t-1}^{2}] = \frac{\alpha_{0}}{1-\alpha_{1}}$이다. 추가적으로, 4차 모멘트 $E[u_{t}^{4}]$도 상수라고 가정하자. 그렇다면
$$E[u_{t}^{4}] = \frac{3\alpha_{0}^{2}(1 + \alpha_{1})}{(1-\alpha_{1})(1-3\alpha_{1}^{2})}$$
- 어떤 확률변수의 kurtosis는 4차 모멘트를 분산의 제곱으로 나눈 것으로 정의된다. 따라서 오차항 $u_{t}$의 분산은
$$3 \frac{1-\alpha_{1}^{2}}{1-3\alpha_{1}^{2}} > 3$$
- kurtosis가 3보다 크다는 것은, 정규분포보다 두꺼운 꼬리를 갖는다는 것을 의미한다. 즉 오차의 조건부분산이 ARCH(1) process를 따를 때 수익률 시계열의 오차항은 두꺼운 꼬리 분포를 가지며, 이는 결국 수익률 시계열의 분포가 두꺼운 꼬리 분포를 가질 개연성을 제공한다.
3. GARCH 모형(Generalized AutoRegressive Conditional Heteroskedasticity)
3.1. GARCH 모형의 도입
- GARCH 모형은 ARCH 모형의 일반화된 버전이다. GARCH 모델은 모델 파라미터 p와 q에 대하여 정의되는데 GARCH(p, q) 모델의 분산 방정식은 아래와 같다.
$$\sigma_{t}^{2} = \alpha_{0} + \beta_{1}\sigma_{t-1}^{2} + ... + \beta_{p}\sigma_{t-p}^{2} + \alpha_{1}u_{t-1}^{2} + ... +\alpha_{q}u_{t-q}^{2}$$
- GARCH 모형은 결국 오차제곱항 $u_{t}^{2}$가 ARMA process라고 하는 것과 동일하다. 왜 그런지 이해하기 위해 간단한 GARCH(1,1) process를 가정하자.
$$\sigma_{t}^{2} = \alpha_{0} + \alpha_{1}u_{t-1}^{2} + \beta_{1}\sigma_{t-1}^{2}$$
- 앞서, $u_{t}^{2} = \sigma_{t}^{2} + w_{t}$라는 것을 보였으므로 이 관계식을 활용하면
$$u_{t}^{2} - w_{t} = \alpha_{0} + \alpha_{1}u_{t-1}^{2} + \beta_{1}(u_{t-1}^{2} -w_{t-1})$$
$$u_{t}^{2} = \alpha_{0} + (\alpha_{1} + \beta_{1})u_{t-1}^{2} +w_{t} - \beta_{1}w_{t-1}$$
- 이는 절편이 존재하는 ARMA(1,1) 모형과 같다는 것을 확인할 수 있다. 일반화해서 표현하면 GARCH(p,q) 모형은 오차제곱항에 대한 ARMA(k,p) 모형을 의미한다. 이때 k = max(p,q)이다.
- 한편, GARCH(p,q) 모형이 약정상성을 충족하기 위한 조건은 분산방정식의 계수합이 1보다 작아야 한다는 것이다.
$$\Sigma_{i=1}^{q}\alpha_{i} + \Sigma_{j=1}^{p}\beta_{j}$$
- GARCH(p,q) 모형의 무조건부 분산은 다음과 같다.
$$Var[u_{t}] = E[u_{t}] = \frac{\alpha_{0}}{1-\alpha_{1}-...-\alpha_{q}-\beta_{1}-...-\beta_{p}}$$
3.2. GARCH 모형의 예측
3.2.1. 평균방정식 추정(ARIMA)
- GARCH 모형은 항상 ARIMA 모형과 함께 정의된다. ARIMA 모형은 수익률의 평균방정식이 되고, 평균방정식의 오차항의 조건부 분산이 GARCH 모형(분산방정식)으로 나타난다.
- 따라서 이론적인 첫 단계는 주어진 수익률 시계열을 fitting하는 ARIMA 모델을 만드는 것이다. 앞서 소개한 KOSPI 지수의 일별 수익률 시계열로부터 ARIMA 모형을 구한다.
- train set을 2021년까지의 수익률 시계열로 두고, AIC를 기준으로 가장 우수한 모형을 찾은 결과 절편이 존재하는 ARIMA(1,0,1) 모형으로 나타났다.
model = pm.auto_arima(y = data_train['Return']
, d = 0
, start_p = 0
, max_p = 3
, start_q = 0
, max_q = 3
, m = 1
, seasonal = False
, stepwise = True
, trace=True
)
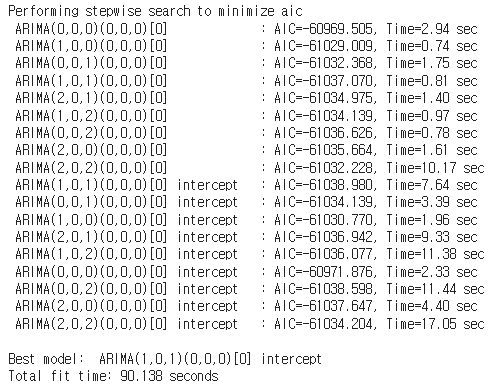
- 수익률의 평균방정식을 나타내는 ARIMA procee는 다음과 같다.
$$r_{t}^{2} = c + \phi_{1}r_{t-1} + \theta_{1}u_{t-1}$$
- ARIMA 모형으로 추정된 수익률 시계열을 그리면 아래와 같다.
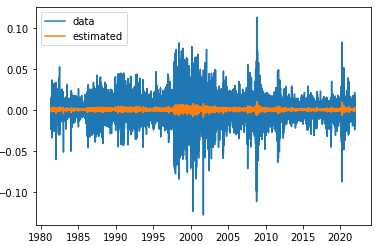
3.2.2. 분산방정식 추정
- 이제 모형을 구했으니 모형의 오차 시계열을 구할 수 있다. 이로부터 조건부분산 $\sigma_{t}^{2}$를 나타내는 분산방정식을 추정한다. 앞서 보았듯이 분산방정식은 다음과 같이 오차제곱항에 대한 방정식으로도 표현할 수 있다. 즉 다음과 같은 GARCH(p,q)의 분산방정식은
$$\sigma_{t}^{2} = \alpha_{0} + \beta_{1}\sigma_{t-1}^{2} + ... + \beta_{p}\sigma_{t-p}^{2} + \alpha_{1}u_{t-1}^{2} + ... +\alpha_{q}u_{t-q}^{2}$$
- k=max(p,q)일 때, 다음과 같이 오차제곱항의 ARIMA(k,q) 방정식으로 나타낼 수 있다.
$$u_{t}^{2} = \alpha_{0} + \Sigma_{i=1}^{k}(\alpha_{i} + \beta_{i})u_{t-1}^{2} +w_{t} - \Sigma_{i=1}^{p}\beta_{1}w_{t-1}$$
- 따라서 굳이 GARCH 라이브러리를 사용하지 않고도, 오차제곱항에 대한 ARIMA 모형을 추정해도 된다. 물론 이 경우에 우리가 추정하려는 것이 $u_{t}^{2}$가 아니라 $\sigma_{t}^{2}$이라는 점을 지적할 수 있다. 그러나 오차제곱항과 조건부분산 간에는 다음과 같은 관계가 있으므로 오차제곱항은 조건부분산과 평균적으로 같다(불편추정량이라는 의미는 아니다).
$$u_{t}^{2} = \sigma_{t}^{2} + w_{t}$$
이때, $w_{t} \sim w.n.(0, \lambda^{2})$
- 그럼 오차제곱항의 ARIMA 모형을 추정하기 위해 모델 파라미터를 결정하자. 오차제곱항의 ACF와 PACF를 그려본 결과 아래와 같았다.
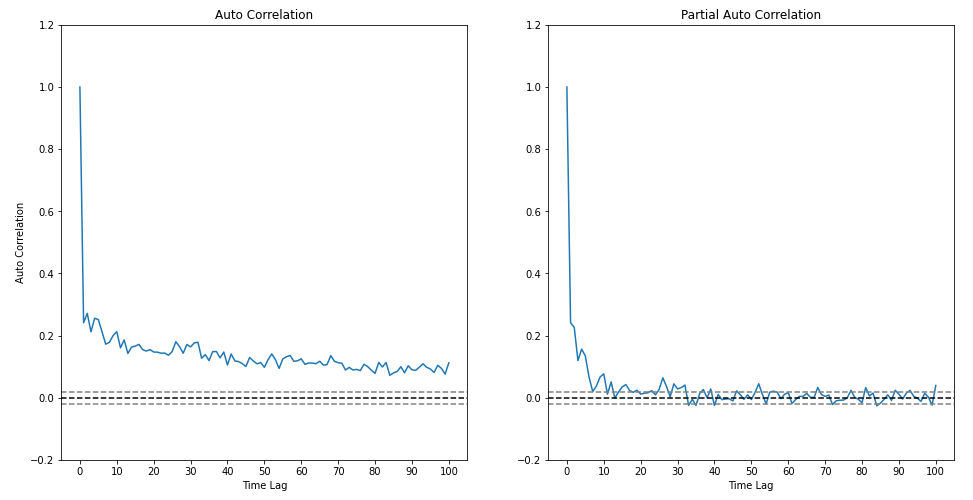
- PACF는 시차 10 정도까지 유의한 수준을 보인다. ACF는 점진적으로 감소하지만 자기상관이 매우 오랫동안 지속되는 것을 알 수 있다. 이렇게 되면 모델의 독립변수 개수가 너무 많아진다. 모델의 독립변수 개수를 고려한 지표인 AIC를 기준으로 한 결과 ARIMA(10,0,10) 모델보다 ARIMA(3,0,3) 모델이 오히려 더 나은 것으로 나타났다. 계산비용의 문제도 있고 해서 ARIMA(3,0,3) 모형으로 오차제곱항을 적합하였다.
- 추정된 ARIMA 모형을 바탕으로, 오차제곱항을 분산의 대용치로 사용한 결과 아래와 같은 분산 시계열을 얻었다. IMF 외환위기, 글로벌 금융위기, 그리고 최근의 코로나 국면에서 분산이 높아지는 직관적인 결과를 얻었다.
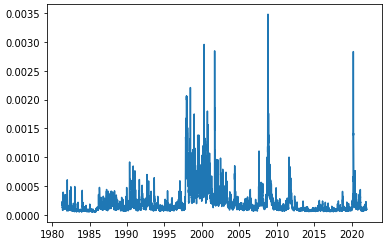
- 아래 그림은 실제 수익률 시계열과, 추정된 수익률 시계열, 그리고 추정된 변동성 시계열(오차제곱항의 제곱근을 대용치로 사용)을 함께 나타난 것이다.
- 두 가지의 시사점을 얻을 수 있다. 첫째, 수익률 시계열 자체는 모형의 추정값과 실제 값 사이의 오차가 매우 크다. 즉 수익률 시계열은 예측할 수 없는 부분들의 영향력이 크다.
- 둘째, 수익률 자체는 예측할 수 없지만 수익률의 오차 분산은 예측할 수 있다. 수익률 예측 모형으로 설명되지 않던 오차들 자체는 예측 불가능했지만 오차들의 변동성이 커지고 작아지는 것은 어느정도 예측할 수 있다.
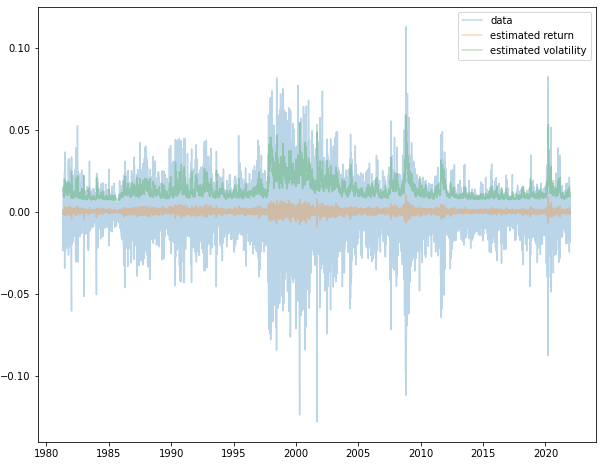
- 유의할 점은 위 그림에서 추정된 변동성과 수익률 시계열을 혼동하지 말아야 한다는 것이다. 변동성은 말그대로 변동성이지 수익률이 아니다. 변동성 시계열이 수익률 시계열과 함께 움직이는 것처럼 보이지만, 어디까지나 수익률(의 오차) 변동성이 커지는 것을 잘 맞추는 것이지 수익률을 맞추는 것이 아니다.
- 약간 비슷한 논의인데, 수익률에서 오차가 차지하는 비중이 매우 크다는 점, 다시 말해 수익률의 예측값은 거의 0으로 수렴하고 수익률은 거의 오차로만 설명된다는 현실적인 점을 반영해서 GARCH 모형에서 오차항을 수익률의 제곱항으로 사용하는 경우도 종종 있다. 즉 다음의 분산방정식에서
$$u_{t}^{2} = \alpha_{0} + \Sigma_{i=1}^{k}(\alpha_{i} + \beta_{i})u_{t-1}^{2} +w_{t} - \Sigma_{i=1}^{p}\beta_{1}w_{t-1}$$
- 오차제곱항 $u_{t}^{2}$를 수익률의 제곱항 $r_{t}^{2}$로 바꾼다.
$$r_{t}^{2} = \alpha_{0} + \Sigma_{i=1}^{k}(\alpha_{i} + \beta_{i})r_{t-1}^{2} +w_{t} - \Sigma_{i=1}^{p}\beta_{1}w_{t-1}$$
3.2.3. Backtesting
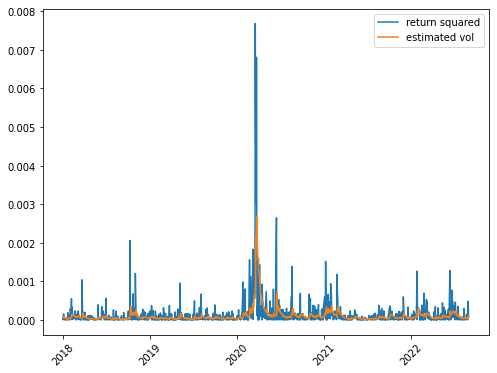
- 2017년까지의 샘플로 훈련 후 2018년 이후의 변동성을 백테스팅한 결과는 아래와 같다(위에서는 2022년을 기준으로 나눴는데 테스트셋이 너무 적은 것 같아서 처음부터 다시 진행했다). 사실 변동성 자체는 라벨이 주어져있는 것이 아니고, 수익률의 평균이 0이라는 가정 하에 수익률 제곱으로 대신 주어진다. 수익률 제곱의 시계열에 대해 백테스팅한 결과 대체로 함께 움직이는 모습을 보여준다.
'시계열&계량경제학' 카테고리의 다른 글
| 시계열 분석 #11: VAR 모형의 이슈들 (0) | 2023.02.15 |
|---|---|
| 시계열 분석 #10 벡터자기회귀(VAR) (0) | 2023.02.14 |
| 시계열 분석 #8 Auto ARIMA & Backtesting (2) | 2023.02.08 |
| 시계열 분석 #7 Box-Jenkins-Method (0) | 2023.02.03 |
| 시계열 분석 #6 정상성 검정 (0) | 2023.02.03 |