- CLM 모형의 가정 중 하나는 오차의 조건부 분포가 정규분포라는 것이다.
- 오차의 조건부 분포에 대한 특별한 가정을 할 수 없는 경우에서 OLS 추정량의 성질을 알아본다.
1. 모형의 가정
- 기본적으로 CLM의 가정과 동일하지만, 정규성 가정만 제외된다.
1) IID: Independently & Identically Distributed
- IID 가정은 데이터셋을 구성하는 각 벡터 [$Y_{t}$, $X_{t1}$, $X_{t2}$, ..., $X_{tk}$]가 독립적이고 동일한 확률분포를 갖는다는 것이다.
2) 선형성: Linearity
- 다음의 식을 성립시키는 $\beta_{*}$가 존재한다.
$$E[Y_{t}|\mathsf{X}_{t}] = \mathsf{X}_{t}^{T}\beta_{*}$$
3) 가역성: Invertibility
- 다음의 행렬이 가역이다.
$$\mathsf{X}^{T}\mathsf{X}$$
4) 비특이성: 완전한 다중공선성의 부재
- 독립변수들 간에 선형종속(Linearly dependent) 관계가 존재하지 않는다는 것이다.
5) 외생성: Exogeneity
$$E[\mathsf{X}_{t}U_{t}] = 0$$
6) 등분산성: Homoskedasticity
- 오차의 조건부 확률분포는 다음과 같다.
$$U_{t}|\mathsf{X}_{t} \sim I.I.D.\,(0, \sigma_{*}^{2})$$
where $$\mathsf{X}_{t} = [X_{t1}, X_{t2}, \cdots , X_{tk}]^{T}$$
2. OLS 추정량의 성질
- 정규성 가정을 하지 않는 경우에도 OLS 추정량은 BLUE가 된다.
- 단 OLS 추정량은 더이상 정규분포를 따르지 않으며, asymptotically하게만 정규분포를 따른다.
- asymptotically하게 정규분포를 따른다는 것은, 표본의 크기가 커질수록 점점 더 OLS 추정량의 분포가 정규분포로 근사된다는 것을 의미한다.
- Asymptotic의 세계로 들어오게 되면, 즉 충분히 큰 규모의 샘플을 다루는 논의에서는 OLS 추정량의 consistency 성질이 더 중요해진다.
- 구체적으로 OLS 추정량이 만족하는 주요한 성질은 다음의 3가지이다.
1) Consistency
$$\hat{\beta}_{n} \rightarrow ^{a.s.} \beta _{*}$$
$$\hat{\sigma}^{2}_{n} \rightarrow ^{a.s.} \sigma^{2}_{*}$$
2) Asympototic Normality
$$\sqrt{n}(\hat{\beta}_{n} - \beta_{*}) \sim ^{A} N(0, \sigma^{2}_{*} E[\mathsf{X}_{t} \mathsf{X}_{t}^{T}]^{-1})$$
- Consistency와 Asymptotic Normality가 성립하기 위해서는, 통계학의 주요한 정리인 대수의 법칙(Law of Large Number)과 중심극한정리(Central Limit Theorem)가 필요하다.
3. OLS 추정량을 활용한 가설 검정
- Asymptotic Normality가 성립하기 때문에, 충분히 큰 규모의 샘플이 주어진 경우에는 여전히 정규분포를 활용한 가설검정이 가능하다.
- 다음의 귀무가설이 참일 때,
$$H_{0}: R\beta_{*}=r$$
- Wald 통계량은 asymptotically하게 카이제곱 분포를 따른다.
$$W_{n} = [R\hat{\beta}_{n}-r]^{T}[\hat{\sigma}^{2}_{n}R(\mathsf{X}^{T}\mathsf{X})^{-1}R^{T}]^{-1}[R\hat{\beta}_{n}-r] \sim \chi^{2}{({r})}$$
- 정규분포 가정을 하지 않더라도, 추정량이 aymptotically하게나마 정규분포를 따른다는 것은 가설 검정을 하기 위해 너무나도 중요한 성질이다.
- 추정량이 어떤 분포를 따르게 되는지 알 수 없다면 가설 검정 자체가 불가능하기 때문이다. 꼭 그 분포가 정규분포일 필요는 없지만, 무슨 분포인지 알기는 해야 한다.
- 바로 이 점이 중심극한정리의 위대함이다. 모집단에 대한 분포 가정을 하지 않고도, 통계량의 확률분포를 이론적으로 완전하게 구할 수 있다. 그리고 통계량의 확률분포를 사용해서, 불확실한 모수에 대해 확률적으로나마(그리고 그 확률이 얼마인지도 알 수 있다) 추론을 할 수 있다.
4. Asymptotic Property에 대한 실험
- 비정규분포 가정 하에서 asymptotic property가 성립하는지 간단한 실험을 해보자.
1) Consistency
- True model이 다음과 같다고 하자.
$$Y_{t} = 3X_{t} + U_{t}$$
where
$$U_{t} \sim (0, 1^{2})$$
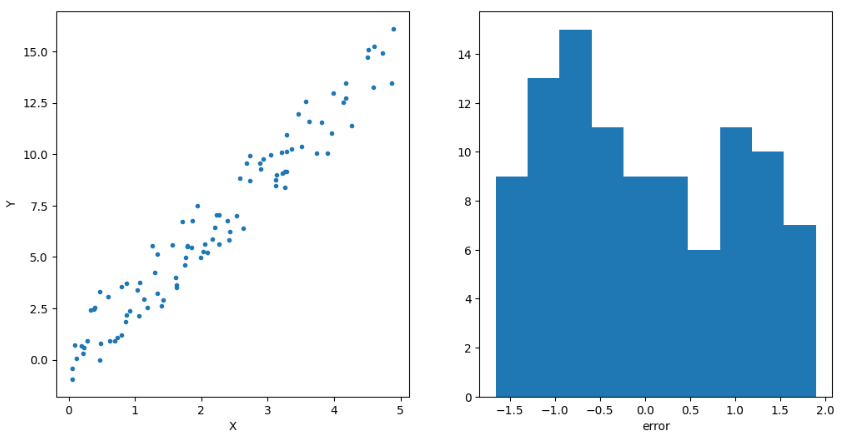
- 샘플 사이즈를 100으로 했을 때, (Y, X)와 오차의 분포는 아래와 같다. 오차의 분포는 전혀 정규분포가 아니다.
- 샘플 사이즈를 2부터 1000까지 키우면서 베타와 시그마에 대한 OLS 추정량을 구했다. 샘플 사이즈가 작을 때에는 모수로부터 괴리가 있다가, 점점 더 모수로 가까워짐을 확인할 수 있다.
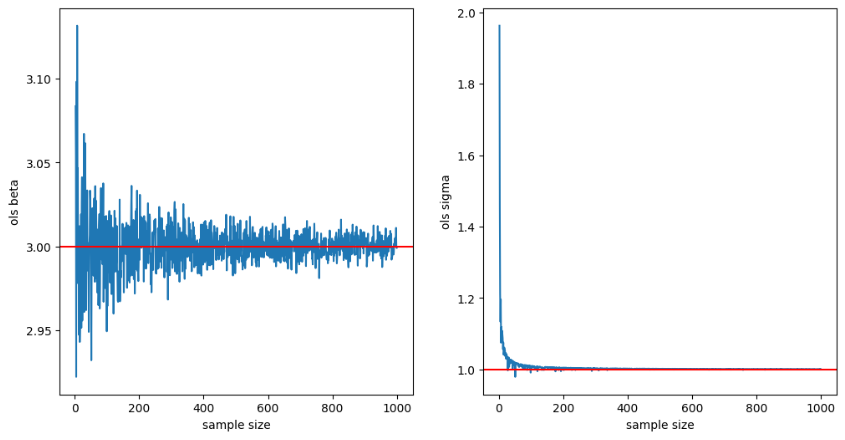
2) Asymptotic Normality
- 다음 통계량이 정규분포를 따르는지 확인해보자.
$$\sqrt{n}(\hat{\beta}_{n} - \beta_{*})$$
- 샘플 사이즈가 5일 때, 시뮬레이션된 분포는 정규분포와는 다소 다르게 생겼다.
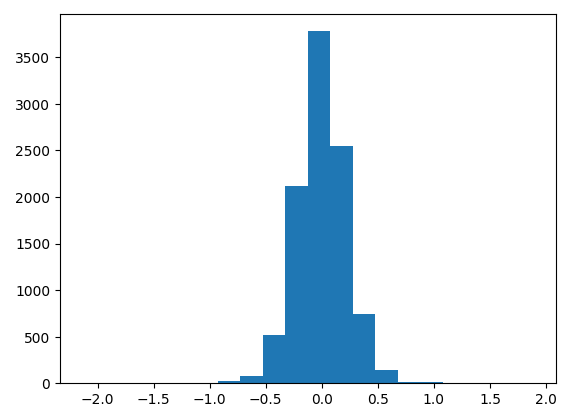
- 샘플 사이즈가 1000일 때, 시뮬레이션된 분포는 정규분포와 훨씬 가까워 보인다.
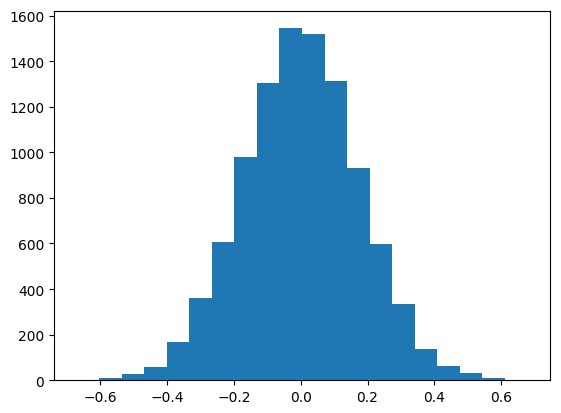
'시계열&계량경제학' 카테고리의 다른 글
| 계량경제학 #4 추정량의 효율성이 왜 문제일까 (0) | 2023.05.20 |
|---|---|
| 계량경제학 #3 이분산 가정 하에서 OLS: HC 추정량과 FGLS (0) | 2023.05.18 |
| 계량경제학 #1 고전적 선형회귀 모형 (0) | 2023.05.11 |
| DeepAR (0) | 2023.02.24 |
| 시계열 분석 #11: VAR 모형의 이슈들 (0) | 2023.02.15 |