1. 시계열의 차분
1.1. 차분
- 차분(differencing)이란 주어진 시계열의 변화분을 구하는 과정을 말한다. 예컨대 t번째 시계열이 $X_{t}$라고 할 때 차분 시계열 $Y_{t}$는 다음을 만족하는 시계열이다.
$${\Delta}X_{t} = X_{t} - X_{t-1}$$
- 가령 다음과 같은 분기별 시계열에 대하여
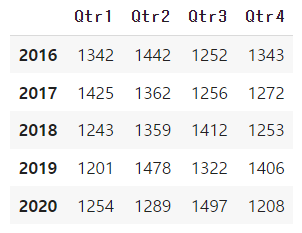
- 차분한 시계열은 아래와 같다. 차분을 수행하면 원 시계열의 첫번째 값은 포함하지 않는다.

- 차분의 시차: 차분이란 일반적으로 시차(time lag)가 1인 차분을 의미하지만 다양한 시차에 대하여 구해질 수 있다. 가령 시차가 2인 차분은 아래와 같다.
$${\Delta}_{2}X_{t} = X_{t} - X_{t-2}$$
- 차분을 거친 시계열을 한 번 더 차분하는 것을 2차 차분이라고 한다('시차가 2인 차분'과, '차분을 두 번한 것'과는 다르다). 이는 d차 차분으로 일반화될 수 있다. 위에서 차분해 얻은 시계열을 한 번 더 차분하면 아래와 같다.

1.2. 차분의 의의
- 어떤 시계열이 추세나 주기를 가지고 있는 비정상(Nonstationary) 시계열일 경우 차분을 수행하면 정상 시계열로 바꿀 수 있다. 예컨대 아래는 삼성전자의 주가 시계열이다. 삼성전자 주가는 장기적으로 증가하는 추세를 가지고 있어 비정상 시계열이다.

- 주가 시계열을 1차 차분하면 비교적 정상성을 갖는 것으로 보이는 시계열을 얻는다. 다만 시간에 대해 분산이 증가하는 형태를 보이므로 이 경우에도 정말 정상성을 갖는다고 할 수 있는지는 불명확하다.

- 사실 주가의 시계열을 정상화할 때는 차분보다는 주가의 수익률을 구하는 방법을 사용한다. 아래는 삼성전가의 주가수익률의 시계열이다.
- 수익률을 구하는 것은 로그차분(Logarithmatic Differentiation)을 사용한다고도 말한다. 테일러 전개식을 활용하면 다음의 식을 증명하는 것이 가능하다.
$$\frac{X_{t} - X_{t-1}}{X_{t-1}} \cong ln(\frac{X_{t}}{X_{t-1}})$$

- 차분을 하는 까닭은 정상성을 갖는 시계열일 경우에 분석 및 예측을 수행하기 더 편리하기 때문이다. 가령 주가를 예측하기 위해 주가의 확률분포의 모수들을 샘플로부터 추정했다고 하자. 그런데 주가가 장기적으로 증가하는 추세를 가지고 있기 때문에 샘플에서 주어진 평균과 분산으로 향후 주가의 확률분포를 추정한다는 것은 불가능하다. 주가가 장기적으로 증가함에 따라 평균과 분산도 계속 증가할 것이기 때문이다.
- 따라서 주가를 차분한다거나, 주가의 수익률을 구한다거나 하여 정상성을 갖는 시계열로 만들어준 후 차분된 주가 시계열의 확률분포를 추정한다. 이 경우에는 평균과 분산이 일정하므로 샘플로부터 시계열의 확률분포를 추정하는 것이 합리적으로 될 수 있다. 그 다음에 수익률 시계열을 역차분(Inverse Difference)하여 원 시계열인 주가를 예측한다.
- 역차분이란 차분된 시계열을 원 시계열로 되돌리는 과정을 말한다. 차분된 시계열이
$${\Delta}X_{t} = X_{t} - X_{t-1}$$
- 일 때, 원 시계열은 다음과 같이 구한다.
$$X_{t} = X_{t-1} + {\Delta}X_{t}$$
- 이때 차분 시계열 ${\Delta}X_{t}$의 확률분포를 추정했으므로, 원 시계열의 확률분포도 추정할 수 있다. 예컨대, 삼성전자의 주가 수익률의 확률분포를 추정하고 이로부터 삼성전자 주가 '수준'의 확률분포를 예측하는 것이다.
2. 시계열의 평활화
2.1. 평활화(Smoothing)
- 평활화란 주어진 시계열의 값을 평탄하게 만드는 작업을 말한다.
- 평활화를 통해서 시계열의 과도한 변동을 제거하고 추세적인 부분만 남겨둘 수가 있다. 이를 통해서 향후 시계열의 추세를 예측하거나, 혹은 이 추세 자체를 제거하여 정상시계열을 만들거나 아니면 시계열의 중간에 누락된 값을 평탄화된 시계열로 예측할 수도 있다.
2.2. 이동평균 평활법
- 평활화는 딱 정해진 방법이 없이 다양한 방법을 사용한다. 가장 기본적인 방법인 이동평균 평활화는 주어진 시계열의 값을 앞뒤의 일정 구간을 두고 평균낸 값으로 대체하는 것이다. 이때 일정구간을 윈도우(window)라고들 표현한다.
- 가령 윈도우를 3이라고 잡으면 원 시계열 $X_{t}$로부터 평활화된 시계열 $Y_{t}$는 다음과 같다.
$$Y_{t} = \frac{X_{t-1} + X_{t} + X_{t+1}}{3}$$
- 삼성전가 주가의 시계열을 30일 이동평균 방법으로 평활화하면 아래와 같다.

- 같은 시계열을 100일 이동평균 방법으로 평활화하면 아래와 같다.
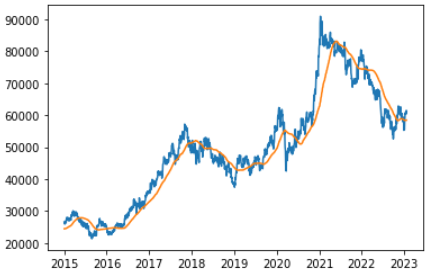
- 평활화를 거친 시계열은 원시계열보다 평탄한 움직임을 보인다는 것을 알 수 있다. 동시에 window가 넓어질수록 평탄화 정도가 높아지는 것도 확인할 수 있다.
2.3. 지수가중 이동평균(EWMA; Exponentially Weighted Moving Average)
- 단순 이동평균의 문제는 현재 값과 이전 값 사이의 가중치가 동일하다는 점이다. 하지만 평활화나 예측을 하는 데 있어서 현재 시계열의 값이 시계열에 대하여 더 많은 정보를 담고 있다는 것은 자명하다. 예컨대 내일의 주가를 예측하는 데 있어서는 오늘의 주가가 어제의 주가보다는 더 많은 정보를 담고 있다. 따라서 오늘의 주가에 더 많은 가중치를 주는 방식이 보다 합리적이라고 할 수 있는데, 이를 구현하는 방법 중 하나가 지수가중 이동평균이다.
- 지수가중 이동평균의 경우 주로 예측기법으로 사용된다. 따라서 시계열의 앞뒤 값으로 평활화하는 것이 아니라 현재값부터 과거 값들만을(미래 값은 사용하지 않음) 사용한다.
- 원 시계열 $X_{t}$로부터 평활화된 시계열 $Y_{t}$는 다음과 같다.
$$Y_{t} = {\lambda}X_{t} + (1-{\lambda})Y_{t-1}$$
- 이때 평활화계수 $\lambda$는 현재의 정보를 얼마나 더 많이 반영할 것인가를 나타내는 파라미터이다. 이 값이 커질수록 현재의 시계열에 더 민감하게 반응하므로 평활화된 시계열의 변동성이 더 커진다.
- 이때 window가 얼마냐고 물을 수 있는데, EWMA 방법은 초기 시계열값으로부터 평활화 시계열을 누적적으로 계산하여 더하는 방식이므로 굳이 window라고 한다면 시계열 전체가 된다.
- 그리고 얻어진 평활화 시계열 자체를 다음기에 대한 예측값으로 사용하기도 한다. 사실 평활화와 예측의 문제는 구분이 되다가도 서로 중첩되는 영역이 많아서 이게 평활화야 예측이야를 구분하려 들기 보다는 그냥 그렇구나 하고 흘려보내는 자세가 필요하다.
- 아래는 삼성전자 주가에 지수가중이동평균 방법을 적용한 것이다. 람다값은 0.1이 사용되었다.
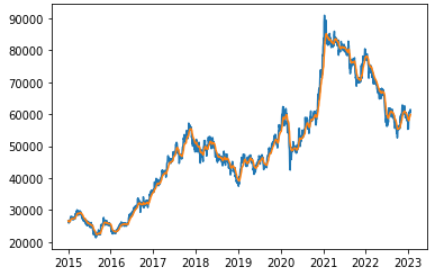
3. 시계열의 요소분해
- 시계열의 요소분해(Decomposition)는 주어진 시계열을 추세변동과 주기변동, 그리고 우연변동으로 분해하는 과정을 말한다. 고전적인 요소분해 방법은 가법(Additive)모형과 승법(Multiplicative)모형으로 구분된다.
3.1. 가법모형
- 가법모형은 주어진 시계열이 추세변동과 주기변동, 그리고 우연변동의 합으로 이루어진 것으로 간주한다. 즉,
$$X_{t} = T_{t} + C_{t} + R_{t}$$
- 이제 어떻게 추세와 주기를 분리할 것인가 고민인데, 사실 방법은 매우 간단하다.
- 추세변동 T는 그냥 이동평균방법으로 구한다.
- 추세가 제거된 시계열로부터 일정 주기마다의 평균을 구하면 주기변동이다.
- 남은 우연변동은 시계열에서 추세변동과 주기변동을 빼서 구한다.
- 가령, 한 기업의 월 매출액 시계열을 요소분해한다면
- 적당한 window를 가지고 이동평균을 구해 추세변동을 계산한다.
- 추세변동을 제거한 시계열로부터 매월의 평균값을 구하면 주기변동이다.
- 추세변동과 주기변동을 모두 빼고 남은 것이 우연변동이다.
- 삼성전자 종가의 시계열을 요소분해하면(주기 = 250거래일) 다음과 같다. 솔직히 믿을 것이 못 된다고 생각한다. 우연변동이 거의 면처럼 두껍게 나오는 것은 우연변동의 변동성이 큰 값으로 추정되었기 때문이다.
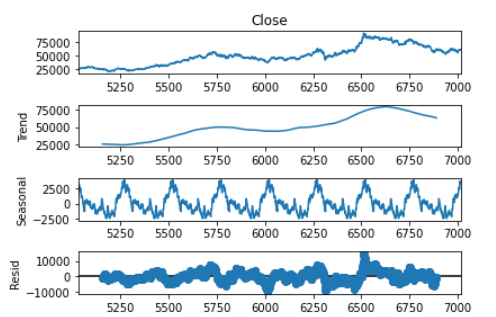
3.2. 승법모형
- 가법모형은 주어진 시계열이 추세변동과 주기변동, 그리고 우연변동의 곱으로 이루어진 것으로 간주한다. 즉,
$$X_{t} = T_{t} * C_{t} * R_{t}$$
- 구하는 방법은 마찬가지로 추세변동을 이동평균 방법으로 구한 다음에
- 원 시계열을 추세변동으로 나누어 추세가 제거된 시계열을 만든다.
- 추세가 제거된 시계열로부터 각 주기마다의 평균을 구하면 주기변동이고
- 추세변동과 주기변동으로 원시계열을 나누어주면 우연변동이 된다.
- 위와 동일한 데이터에 적용한 예시는 아래와 같다. 치명적인 것은 원 시계열이 항상 플러스의 값을 가지면 우연변동이 항상 플러스의 값으로 나온다는 것이다.
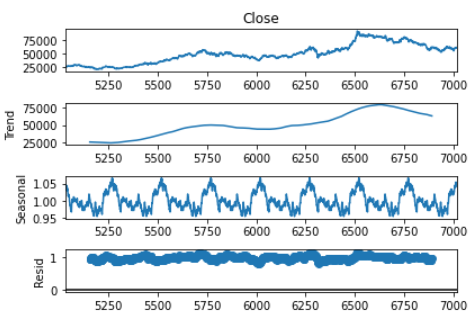
3.3. HP 필터
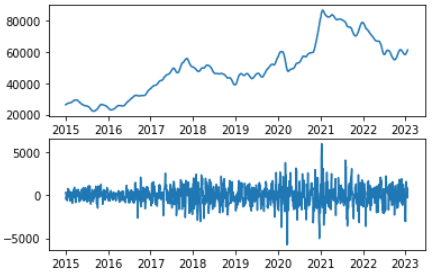
- HP(Hodrick–Prescott) 필터 모형은 고전적 방법보다 조금 더 자주 쓰인다. HP 필터 모형은 시계열의 추세와, 추세로 설명되지 않는 단기적 변동 요인으로 분해한다. 모형은 아래와 같다.
$$Y_{t} = T_{t} + C_{t}$$
- 모형 자체는 가법 모형과 비슷하지만, 추세변동을 구할 때 단순이동평균을 사용하지 않는다. 그보다 시계열의 특성을 잘 표현하기 위한 비용함수를 정의하고, 이 비용함수를 최소화하는 추세변동을 구한다.
$${\min}_{Τ_{t}} [{\Sigma}_{t=1}^{n}(Y_{t}−Τ_{t})^{2} + \lambda{\Sigma}_{t=2}^{n-1}{(T_{t+1}−T_{t}) − (T_{t}−T_{t−1})}^2]$$
- 비용함수의 첫번째 항은 원시계열을 추세가 잘 반영해야 한다는 것을 나타내고, 두번째 항은 연이은 두 차분 시계열이 너무 괴리되어서는 안 된다는 즉 평탄화가 이루어져야 한다는 것을 나타낸다. 따라서 두번째 항에 붙은 계수 람다를 평탄화계수라고 한다.
- 삼성전자 주가에 HP 필터(람다 = 1600)를 적용해 얻은 결과는 아래와 같다.
'시계열&계량경제학' 카테고리의 다른 글
| 시계열 분석 #6 정상성 검정 (0) | 2023.02.03 |
|---|---|
| 시계열 분석 #5 MA process와 ARMA process (0) | 2023.02.03 |
| 시계열 분석 #4 white noise와 AR process (0) | 2023.02.02 |
| 시계열 분석 #3 자기상관 (0) | 2023.02.01 |
| 시계열 분석 #1 시계열의 정상성과 유형 (1) | 2023.01.24 |